题目内容
【题目】已知数列![]() ,
, ![]() ,
, ![]() ,
, ![]() 满足
满足![]() ,且当
,且当![]() 时,
时, ![]() ,令
,令![]() .
.
(Ⅰ)写出![]() 的所有可能的值.
的所有可能的值.
(Ⅱ)求![]() 的最大值.
的最大值.
(Ⅲ)是否存在数列![]() ,使得
,使得![]() ?若存在,求出数列
?若存在,求出数列![]() ;若不存在,说明理由.
;若不存在,说明理由.
【答案】(1)![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;(2)
;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】试题分析:(Ⅰ)由题设可知当i=5时,可得满足条件的数列![]() 的所有可能情况;
的所有可能情况;
(Ⅱ)确定当![]() ,
, ![]() ,
, ![]() 的前
的前![]() 项取
项取![]() ,后
,后![]() 项取
项取![]() 时
时![]() 最大,此时
最大,此时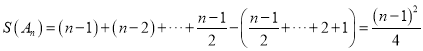 .
.
(Ⅲ)由(Ⅱ)可以知道,如果![]() ,
, ![]() ,
, ![]() 的前
的前![]() 项中恰有
项中恰有![]() 项,
项, ![]() ,
, ![]() ,
, ![]() 取
取![]() ,
, ![]() ,
, ![]() ,
, ![]() 的后
的后![]() 项中恰有
项中恰有![]() 项
项![]() ,
, ![]() ,
, ![]() 取
取![]() ,则
,则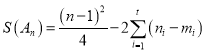 ,利用条件,分n是奇数与偶数,即可得到结论.
,利用条件,分n是奇数与偶数,即可得到结论.
试题解析:(![]() )有题设,满足条件的数列
)有题设,满足条件的数列![]() 的所有可能情况有:
的所有可能情况有:
①![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,此时
,此时![]() ;
;
②![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,此时
,此时![]() ;
;
③![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,此时
,此时![]() ;
;
④![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,此时
,此时![]() ;
;
⑤![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,此时
,此时![]() ;
;
⑥![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,此时
,此时![]() .
.
∴![]() 的所有可能的值为
的所有可能的值为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(![]() ) 由
) 由![]() ,可设
,可设![]() ,则
,则![]() 或
或![]() .
.
∵![]() ,∴
,∴![]()
![]() .
.
∵![]() ,
,
∴![]() ,且
,且![]() 为奇数,
为奇数, ![]() ,
, ![]() 是由
是由![]() 个
个![]() 和
和![]() 个
个![]() 构成数列.
构成数列.
∴![]()
![]() .
.
则当![]() ,
, ![]() ,
, ![]() 的前
的前![]() 项取
项取![]() ,后
,后![]() 项取
项取![]() 时
时![]() 最大,
最大,
此时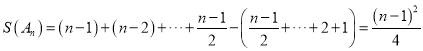 .
.
证明如下:
假设![]() ,
, ![]() 的前
的前![]() 项中恰有
项中恰有![]() 项
项![]() ,
, ![]() ,
, ![]() 取
取![]() ,则
,则![]() ,
, ![]() ,
, ![]() 的后
的后![]() 项中恰有
项中恰有![]() 项
项![]() ,
, ![]() 取
取![]() ,其中
,其中![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
∴![]()
![]()
![]()
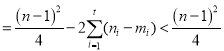 .
.
∴![]() 的最大值为
的最大值为![]() .
.
(![]() )由(
)由(![]() )可知,如果
)可知,如果![]() ,
, ![]() ,
, ![]() 的前
的前![]() 项中恰有
项中恰有![]() 项,
项, ![]() ,
, ![]() ,
, ![]() 取
取![]() ,
, ![]() ,
, ![]() ,
, ![]() 的后
的后![]() 项中恰有
项中恰有![]() 项
项![]() ,
, ![]() ,
, ![]() 取
取![]() ,则
,则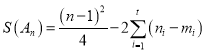 ,若
,若![]() ,
,
则![]() .
.
∵![]() 是奇数,∴
是奇数,∴![]() 是奇数,而
是奇数,而![]() 是偶数.
是偶数.
∴不存在数列![]() ,使得
,使得![]() .
.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目