题目内容
2.(1)已知直线l1:ax+2y+6=0和直线${l_2}:x+(a-1)y+{a^2}-1=0$.当l1∥l2时,求a的值.(2)已知点P(2,-1),求过P点且与原点距离最大的直线l的方程,并求出最大距离.
分析 (1)利用直线平行的性质求解.
(2)过P点与原点O距离最大的直线是过P点且与PO垂直的直线,求出斜率,利用点斜式可得直线方程,再利用点到直线的距离公式求出距离即可;
解答 解:(1)由A1B2-A2B1=0,得a(a-1)-1×2=0,
由B1C2-B2C1≠0,得2(a2-1)-6(a-1)≠0,∴a=-1
(2)过P点且与原点距离最大的直线,是过P点且与OP垂直的直线,
由l⊥OP得klkOP=-1.所以kl=2.
由直线方程的点斜式得y+1=2(x-2),即2x-y-5=0,
所以直线2x-y-5=0是过P点且与原点距离最大的直线,最大距离为$d=\frac{{|{-5}|}}{{\sqrt{5}}}=\sqrt{5}$.
点评 本题考查实数值的求法,是基础题,解题时要认真审题,注意直线平行的性质的灵活运用.

练习册系列答案
相关题目
12.设函数f(x)=($\frac{sinB}{cosA}$)x+($\frac{sinA}{cosB}$)x,其中A、B为△ABC的内角,如果对任意x>0都有f(x)<2,那么( )
| A. | 0<A+B<$\frac{π}{4}$ | B. | 0<A+B<$\frac{π}{2}$ | C. | $\frac{π}{2}$<A+B<$\frac{3π}{4}$ | D. | A+B>$\frac{π}{2}$ |
13.化简$\frac{cos2α}{{4{{sin}^2}(\frac{π}{4}+α)tan(\frac{π}{4}-α)}}$=( )
| A. | cosα | B. | sinα | C. | 1 | D. | $\frac{1}{2}$ |
17.如图,将正方形ABCD沿对角线AC折成一个直二面角,则异面直线AB和CD所成的角是( )
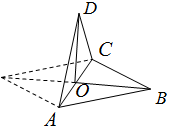

| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
14.已知函数$f(x)=sin(\frac{π}{3}x+φ)(|φ|<\frac{π}{2})$的图象关于直线x=1对称,把f(x)的图象向右平移3个单位长度后,所得图象对应的函数解析式为( )
| A. | y=sin($\frac{π}{3}$x+$\frac{π}{6}$) | B. | y=sin($\frac{π}{3}$x-$\frac{π}{6}$) | C. | y=cos($\frac{π}{3}$x+$\frac{π}{6}$) | D. | y=sin($\frac{π}{3}$x-$\frac{5π}{6}$) |
11.一条光线从点(-2,-3)射出,经y轴反射后与圆(x+3)2+(y-2)2=1相切,则入射光线所在直线的斜率为( )
| A. | $\frac{3}{2}$或$\frac{2}{3}$ | B. | $\frac{4}{3}$或$\frac{3}{4}$ | C. | $\frac{5}{3}或\frac{3}{5}$ | D. | $\frac{5}{4}或\frac{4}{5}$ |
