题目内容
已知函数: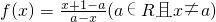 .
.
(1)证明:f(x)+2+f(2a-x)=0对定义域内的所有x都成立;
(2)当f(x)的定义域为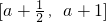 时,求证:f(x)的值域为[-3,-2];
时,求证:f(x)的值域为[-3,-2];
(3)(理)设函数g(x)=x2+|(x-a)f(x)|,求g(x)的最小值.
(4)(文)设函数g(x)=x2+(x-a)f(x),其中x≤a-1,求g(x)的最小值.
解:(1)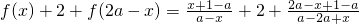
=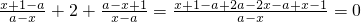
∴结论成立
(2)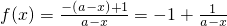
当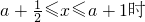 ,
,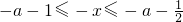 ,
,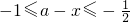 ,
,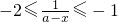 ,
,
∴ 即f(x)值域为[-3,-2].
即f(x)值域为[-3,-2].
(3)(理)g(x)=x2+|x+1-a|(x≠a)
①当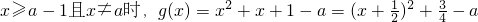 .
.
如果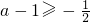 即
即 时,则函数在[a-1,a)和(a,+∞)上单调递增,∴g(x)min=g(a-1)=(a-1)2
时,则函数在[a-1,a)和(a,+∞)上单调递增,∴g(x)min=g(a-1)=(a-1)2
如果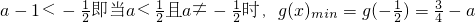 .当
.当 时,g(x)最小值不存在.
时,g(x)最小值不存在.
②当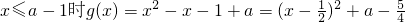 ,
,
如果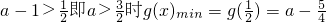 .
.
如果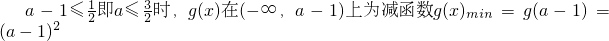 .
.
当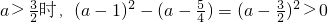 .
.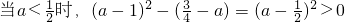 .
.
综合得:当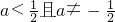 时,g(x)最小值是
时,g(x)最小值是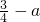 ;当
;当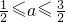 时,g(x)最小值是(a-1)2;当
时,g(x)最小值是(a-1)2;当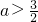 时,g(x)最小值为
时,g(x)最小值为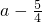 ;当
;当 时,g(x)最小值不存在.
时,g(x)最小值不存在.
(文)同②
分析:(1)利用函数函数: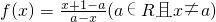 .直接代入化简即可;
.直接代入化简即可;
(2)化简函数的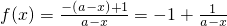 ,根据定义域为
,根据定义域为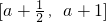 ,
,
可确定f(x)的值域为[-3,-2];
(3)利用分类讨论,将绝对值符号化去,再利用二次函数配方法求解,应注意函数定义域与函数对称轴之间的关系.
点评:本题以函数为载体,考查函数的性质,考查函数的值域,同时考查学生分析解决问题的能力,有一定的难度.
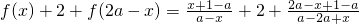
=
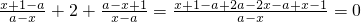
∴结论成立
(2)
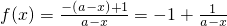
当
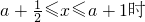 ,
,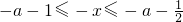 ,
,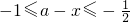 ,
,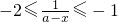 ,
,∴
 即f(x)值域为[-3,-2].
即f(x)值域为[-3,-2].(3)(理)g(x)=x2+|x+1-a|(x≠a)
①当
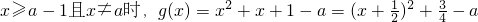 .
.如果
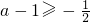 即
即 时,则函数在[a-1,a)和(a,+∞)上单调递增,∴g(x)min=g(a-1)=(a-1)2
时,则函数在[a-1,a)和(a,+∞)上单调递增,∴g(x)min=g(a-1)=(a-1)2如果
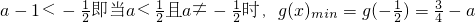 .当
.当 时,g(x)最小值不存在.
时,g(x)最小值不存在.②当
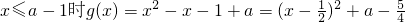 ,
,如果
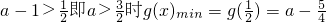 .
.如果
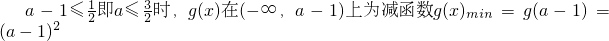 .
.当
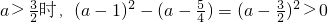 .
.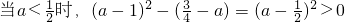 .
.综合得:当
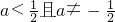 时,g(x)最小值是
时,g(x)最小值是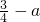 ;当
;当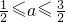 时,g(x)最小值是(a-1)2;当
时,g(x)最小值是(a-1)2;当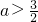 时,g(x)最小值为
时,g(x)最小值为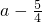 ;当
;当 时,g(x)最小值不存在.
时,g(x)最小值不存在.(文)同②
分析:(1)利用函数函数:
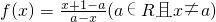 .直接代入化简即可;
.直接代入化简即可;(2)化简函数的
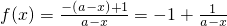 ,根据定义域为
,根据定义域为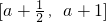 ,
,可确定f(x)的值域为[-3,-2];
(3)利用分类讨论,将绝对值符号化去,再利用二次函数配方法求解,应注意函数定义域与函数对称轴之间的关系.
点评:本题以函数为载体,考查函数的性质,考查函数的值域,同时考查学生分析解决问题的能力,有一定的难度.

练习册系列答案
相关题目