题目内容
已知函数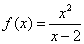
(x∈R，且x≠2)．
(1)求f(x)的单调区间；
(2)若函数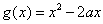
与函数f(x)在x∈[0，1]上有相同的值域，求a的值．
解：(1)f(x)＝
令x－2＝t，由于y＝t＋
＋4在(－∞，－2)，(2，＋∞)内单调递增，在(－2，0)，(0，2)内单调递减，∴容易求得f(x)的单调递增区间为
(－∞，0)，(4，＋∞)；单调递减区间为(0，2)，(2，4)．
(2)∵f(x)在x∈[0，1]上单调递减，∴其值域为[－1，0]，
即x∈[0，1]时，g(x)∈[－1，0]．
∵g(0)＝0为最大值，∴最小值只能为g(1)或g(a)，
综上得a＝1
练习册系列答案
相关题目
在
处取得极大值10，则
= ．
＝lg x，则f(21)＝___________________.
时，从 “
到
”时，左边应增添的式子是 （ ）
B. 
C. 
D. 
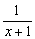在（－∞，－1）∪（－1，＋∞）上是减函数；③函数y =
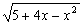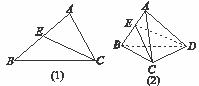
的单调区间是［－2，+∞）；④已知f（x）在R上是增函数，若a+b＞0，则有f（a）+f（b）＞f（－a）+f（－b）.其中正确命题的序号是______________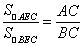
.将这个结论类比到空间：在三棱锥A－BCD中，平面DEC平分二面角A－CD－B且与AB交于E，则类比的结论为
＝________．
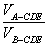满足：
，则函数
上的最小值为 ．
，
，
，则
、
、
的大小关系是 .
的单调递减区间为 ．