题目内容
【题目】已知条件P:①是奇函数;②值域为R;③函数图象经过第四象限。则下列函数中满足条件Р的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
利用奇函数的定义和值域的定义及其图象逐一进行判断即可.
对于A选项:![]() ,
,
又因为![]() 的定义域为
的定义域为![]() ,关于原点对称,
,关于原点对称,
所以![]() 为定义在
为定义在![]() 上的偶函数,
上的偶函数,
故选项A不符合题意;
对于B选项: ![]() 的定义域为
的定义域为![]() ,
,
所以![]() 的定义域关于原点对称,
的定义域关于原点对称,
又因为![]() ,
,
所以![]() 为奇函数,①成立,
为奇函数,①成立,
当![]() 时,
时,![]() ,
,
当![]() 时,
时, ,
,
故![]() 的值域为
的值域为![]() ,②不成立,
,②不成立,
所以选项B不符合题意;
对于C选项:因为![]() ,
,
所以![]() 的定义域为
的定义域为![]() ,关于原点对称,
,关于原点对称,
又因为![]() ,
,
故![]() 为奇函数,
为奇函数,
因为函数![]() 的图象是由幂函数
的图象是由幂函数![]() 的图象关于
的图象关于![]() 轴翻折得到的,
轴翻折得到的,
所以函数![]() 值域为
值域为![]() ,图像经过第四象限,
,图像经过第四象限,
所以选项C符合题意;
对于D选项:因为![]() 的定义域为
的定义域为![]() ,关于原点对称,
,关于原点对称,
又因为![]() ,
,
所以函数![]() 为奇函数,
为奇函数,
因为![]() ,
,
所以函数![]() 的值域为
的值域为![]() ,不符合题意.
,不符合题意.
所以选项D不符合题意;
故选: C

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
【题目】某大型单位举行了一次全体员工都参加的考试,从中随机抽取了20人的分数.以下茎叶图记录了他们的考试分数(以十位数字为茎,个位数字为叶):

若分数不低于95分,则称该员工的成绩为“优秀”.
(1)从这20人中任取3人,求恰有1人成绩“优秀”的概率;
(2)根据这20人的分数补全下方的频率分布表和频率分布直方图,并根据频率分布直方图解决下面的问题.
组别 | 分组 | 频数 | 频率 |
|
1 |
| |||
2 |
| |||
3 |
| |||
4 |
|
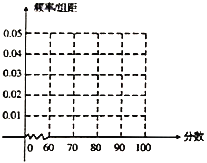
①估计所有员工的平均分数(同一组中的数据用该组区间的中点值作代表);
②若从所有员工中任选3人,记![]() 表示抽到的员工成绩为“优秀”的人数,求
表示抽到的员工成绩为“优秀”的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.