题目内容
对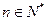 ,不等式
,不等式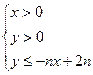 所表示的平面区域为
所表示的平面区域为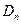 ,把
,把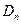 内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:
内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列: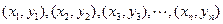
(1)求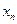 ,
,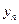 ;
;
(2)数列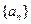 满足
满足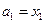 ,且
,且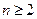 时
时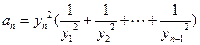 .证明当
.证明当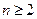 时,
时,
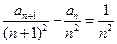 ;
;
(3)在(2)的条件下,试比较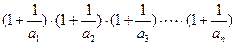 与4的大小关系.
与4的大小关系.
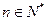 ,不等式
,不等式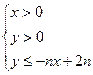 所表示的平面区域为
所表示的平面区域为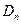 ,把
,把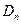 内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:
内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列: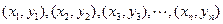
(1)求
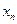 ,
,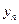 ;
;(2)数列
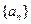 满足
满足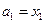 ,且
,且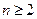 时
时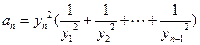 .证明当
.证明当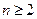 时,
时,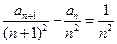 ;
;(3)在(2)的条件下,试比较
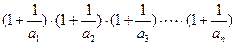 与4的大小关系.
与4的大小关系.(1) (2)证略(3)
(2)证略(3)
 (2)证略(3)
(2)证略(3)
(1)解: ,又
,又 且
且 ,∴
,∴ ……(2分)
……(2分)
故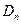 内的整点都落在直线
内的整点都落在直线 上且
上且 ,故
,故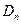 内的整点按其到原点的距离从近到远排成的点列为
内的整点按其到原点的距离从近到远排成的点列为 ,∴
,∴ . ……(4分)
. ……(4分)
(2)证:当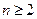 时,
时,
由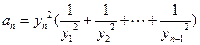 ,得
,得 ,
,
即 ……①
……①
∴ ……② ……(6分)
……② ……(6分)
②式减①式,有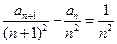 ,得证. ……(8分)
,得证. ……(8分)
(3)解:当 时,
时,  ;
;
当 时,
时,  ,
,
由(2)知,当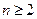 时,
时, , ……(10分)
, ……(10分)
∴当 时,
时,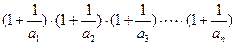



∵ , ……(12分)
, ……(12分)
∴上式 ,
,
 ,又
,又 且
且 ,∴
,∴ ……(2分)
……(2分)故
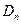 内的整点都落在直线
内的整点都落在直线 上且
上且 ,故
,故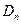 内的整点按其到原点的距离从近到远排成的点列为
内的整点按其到原点的距离从近到远排成的点列为 ,∴
,∴ . ……(4分)
. ……(4分)(2)证:当
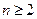 时,
时,由
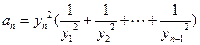 ,得
,得 ,
,即
 ……①
……① ∴
 ……② ……(6分)
……② ……(6分)②式减①式,有
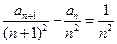 ,得证. ……(8分)
,得证. ……(8分)(3)解:当
 时,
时,  ;
;当
 时,
时,  ,
, 由(2)知,当
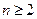 时,
时, , ……(10分)
, ……(10分)∴当
 时,
时,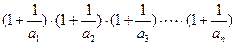



∵
 , ……(12分)
, ……(12分)∴上式
 ,
,
练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
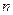 行的第二个数为
行的第二个数为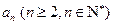 ,
,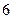 个数字;
个数字;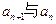 的关系式并求出
的关系式并求出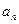 的通项公式;
的通项公式;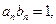 求证:
求证: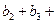 …
…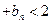
 满足条件:
满足条件: ,且
,且 )
)
 的前
的前 项和为
项和为 ,数列
,数列 满足
满足 ,且
,且 ,
, .
. 的表达式;
的表达式; ,求数列
,求数列 的前
的前 .
.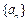 的前
的前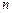 项和为
项和为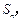 且
且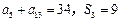 .
.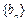 的通项公式为
的通项公式为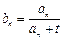 ,问: 是否存在正整数t,使得
,问: 是否存在正整数t,使得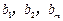
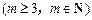 成等差数列?若存在,求出t和m的值;若不存在,请说明理由.
成等差数列?若存在,求出t和m的值;若不存在,请说明理由. 是一次函数,且
是一次函数,且 ,
, ,其中
,其中 自然对数的底。(1)求函数
自然对数的底。(1)求函数 中,
中, ,
, ,求数列
,求数列 满足
满足 ,试求数列
,试求数列 项和
项和 。
。

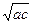
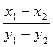 =____________.
=____________.