题目内容
已知数列{an}中,a1=
,an+1=
an(n=1,2,…).计算a2,a3,a4的值,根据计算结果,猜想an的通项公式,并用数学归纳法进行证明.
| ||
| 2 |
|
根据已知,a2=
,a3=
=
,a4=
,
猜测an=
.…(3分)
证明:①当n=1时,由已知,左边=
,右边=
=
,猜想成立.…(4分)
②假设当n=k(k∈N*)时猜想成立,即ak=
,…(5分)
那么,ak+1=
ak=
•
=
=
=
,…(7分)
所以,当n=k+1时,猜想也成立.
根据①和②,可知猜想对于任何n∈N*都成立.…(8分)
| ||
| 3 |
| ||
| 4 |
| 1 |
| 2 |
| ||
| 5 |
猜测an=
| ||
| n+1 |
证明:①当n=1时,由已知,左边=
| ||
| 2 |
| ||
| 1+1 |
| ||
| 2 |
②假设当n=k(k∈N*)时猜想成立,即ak=
| ||
| k+1 |
那么,ak+1=
|
|
| ||
| k+1 |
| 1 | ||
|
| ||
| k+2 |
| ||
| (k+1)+1 |
所以,当n=k+1时,猜想也成立.
根据①和②,可知猜想对于任何n∈N*都成立.…(8分)

练习册系列答案
相关题目
 中,
中, ,求数列
,求数列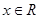 ,
, 恒成立(其中
恒成立(其中 ),求
),求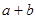 的最大值.
的最大值. ,
,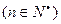
 ,则
,则 的最小值是 .
的最小值是 .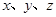 满足
满足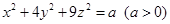 ,且
,且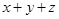 的最大值是7,求
的最大值是7,求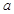 的值.
的值. ,将它沿高AD翻折,使点B 与点C间的距离为
,将它沿高AD翻折,使点B 与点C间的距离为