题目内容
“
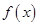在[a,b]上为单调函数”是“函数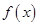在[a,b]上有最大值和最小值”的( )
| A．充分非必要条件 | B．必要非充分条件 |
| C．充要条件 | D．既不充分也非必要条件 |
A
解析试题分析：由“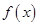在[a,b]上为单调函数”可以得出“函数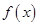在[a,b]上有最大值和最小值”，但是由“函数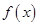在[a,b]上有最大值和最小值”，得不出函数单调，不单调也一样有最大值和最小值，只要是闭区间上的连续函数都有最大值和最小值.
考点：本小题主要考查函数的单调性与函数的最值之间的关系.
点评：闭区间上的连续函数一定有最大值和最小值，而与单调与否无关.
练习册系列答案
天天练口算系列答案
相关题目
已知a，b，c∈R，命题“若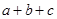
=3，则
≥3”的否命题是（ ）
| A．若a+b+c≠3，则<3 | B．若a+b+c=3，则<3 |
| C．若a+b+c≠3，则≥3 | D．若≥3，则a+b+c=3 |
设
R，则“
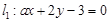”是“直线
与直线
平行”的( )条件
| A．充分不必要 | B．必要不充分 |
| C．充要 | D．既不充分也不必要 |
下列四个判断：
①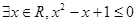
；
②已知随机变量X服从正态分布N（3，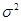
），P（X≤6）=0．72，则P（X≤0）=0．28;
③已知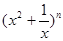
的展开式的各项系数和为32，则展开式中x项的系数为20；
④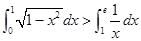
其中正确的个数有：
| A．1个 | B．2个 | C．3个 | D．4个 |
给出下列命题：①a＞b⇒ac2＞bc2； ②a＞|b|⇒a2＞b2； ③a＞b⇒a3＞b3；
④|a|＞b⇒a2＞b2.其中正确的命题是( )．
| A．①② | B．②③ | C．③④ | D．①④ |
可导函数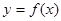
在一点的导数值为
是函数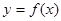在这点取极值的（ ）
| A．充分不必要条件 | B．必要不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |
若命题p的逆命题是q，命题p的逆否命题是r, 则命题q与r的关系是（ ）
| A．互为逆命题 | B．互为否命题 | C．互为逆否命题 | D．不能确定 |
设a,b,c分别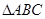
是的三个内角
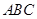所对的边，若
,
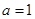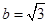则
是
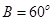的（ ）
| A．充分不必要条件 | B．必要不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |
“a = 1”是“复数
（
，i为虚数单位）是纯虚数”的
| A．充分不必要条件 | B．必要不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |