题目内容
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线方程是
处的切线方程是![]() .
.
(Ⅰ)求实数![]() ,
,![]() 的值;
的值;
(Ⅱ)若函数![]() 有两个不同的零点
有两个不同的零点![]() ,
,![]() ,求证:
,求证:![]() .
.
【答案】(Ⅰ)![]() ,
,![]() ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
【解析】
(Ⅰ)根据导数的几何意义,![]() 点处的导数就是该点切线的斜率,再根据该切点既在曲线上也在直线上,列式即可得解;
点处的导数就是该点切线的斜率,再根据该切点既在曲线上也在直线上,列式即可得解;
(Ⅱ)求出![]() 的解析式及其单调性,当
的解析式及其单调性,当![]() 时,
时,![]() ,
,![]() 为增函数;
为增函数;
![]() 时,
时,![]() ,
,![]() 为减函数,由函数
为减函数,由函数![]() 有两个不同的零点,则
有两个不同的零点,则![]() ,
,![]() 满足
满足![]() ,构造函数
,构造函数![]() ,再根据
,再根据![]() 的单调性即可得出
的单调性即可得出![]() ,
,![]() 的关系.
的关系.
(Ⅰ)由![]() 求导,得
求导,得![]() ,
,
由切线方程![]() 知,切点为
知,切点为![]() ,
,
切线斜率为![]() ,
,
所以 解得
解得![]() ,
,![]() .
.
(Ⅱ)由(Ⅰ)知![]() ,
,
![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,
,![]() 为增函数;
为增函数;
![]() 时,
时,![]() ,
,![]() 为减函数.
为减函数.
所以![]() 时,函数
时,函数![]() 取得极大值.
取得极大值.
又易知![]() ,
,![]() ,
,![]() ,
,
所以函数![]() 的两个不同的零点
的两个不同的零点![]() ,
,![]() 满足
满足![]() ,
,
构造函数![]() ,
,
即![]() ,
,
![]() .
.
当![]() 时,
时,![]() ,所以
,所以![]() 为
为![]() 上的增函数,
上的增函数,
因为![]() ,所以
,所以![]() ,
,
即![]() ,即
,即![]() ,
,
因为![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() ,而
,而![]() ,且
,且![]() 在区间
在区间![]() 上单调递减,
上单调递减,
所以由![]() 可得
可得![]() ,
,
即![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某中学从甲乙两个教师所教班级的学生中随机抽取100人,每人分别对两个教师进行评分,满分均为100分,整理评分数据,将分数以10为组距分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .得到甲教师的频率分布直方图,和乙教师的频数分布表:
.得到甲教师的频率分布直方图,和乙教师的频数分布表:
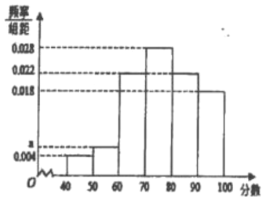
乙教师分数频数分布表 | |
分数区间 | 频数 |
| 3 |
| 3 |
| 15 |
| 19 |
| 35 |
| 25 |
(1)在抽样的100人中,求对甲教师的评分低于70分的人数;
(2)从对乙教师的评分在![]() 范围内的人中随机选出2人,求2人评分均在
范围内的人中随机选出2人,求2人评分均在![]() 范围内的概率;
范围内的概率;
(3)如果该校以学生对老师评分的平均数是否大于80分作为衡量一个教师是否可评为该年度该校优秀教师的标准,则甲、乙两个教师中哪一个可评为年度该校优秀教师?(精确到0.1)