题目内容

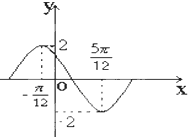
如图是函数y=Asin（φx+φ）在一个周期内的图象，此函数的解析式为可为（　　）
A．y=2sin（2x+
π
3
B．y=2sin（2x+
2π
3
C．y=2sin（
x
2
-
π
3
）		D．y=2sin（2x-
π
3
）
由于最大值为2，所以A=2；又
T
2
=
5
12
-(-
π
12
)=
π
2
⇒T=π⇒
2π
ω
=π⇒ω=2．
∴y=2sin（2x+φ），将点（
π
12
，2）代入函数的解析式求得sin(
π
6
+φ)=1，
结合点的位置，知
π
6
+φ=
π
2
⇒φ=
π
3
，
∴函数的 解析式为可为y=2sin(2x+
π
3
)，
故选B．
练习册系列答案
相关题目
（本小题满分14分）函数
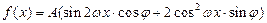
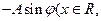
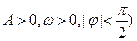的图象在y轴右侧的第一个最高点（即函数取得最大值的点）为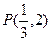，在原点右侧与x轴的第一个交点为Q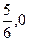（）. 求：（1）函数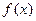的表达式；  （2）函数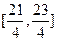在区间上的对称轴的方程.
若α，β都是第一象限角，且α＜β，那么（　　）
A．sinα＞sinβB．sinβ＞sinα
C．sinα≥sinβD．sinα与sinβ的大小不定
函 f（x）=Asin（ωx+φ）（A＞0，ω＞0，0≤φ＜2π）在R上的部分图象如图所示，则 f（x）=______．
如图为f（x）=Asin（ωx+ϕ）（A＞0，?＞0，ϕ∈（-π，0））的图象的一段，
（Ⅰ）求其解析式．
（Ⅱ）将f（x）图象上所有的点纵坐标不变，横坐标放大到原来的2倍，然后再将新的图象向左平移
π
2
个单位，得到函数g（x）的图象，求函数g（x）在x∈[0，
π
2
]的值域．
已知向量
a
=(
3
sinωx，cosωx)，
b
=(cosωx，-cosωx)，(ω＞0)，函数f(x)=
a
•
b
+
1
2
的图象的两相邻对称轴间的距离为
π
4
，
（1）求ω；
（2）若x∈(0，
5
12
π)时，求函数f（x）的单调递增区间；
（3）若cosx≥
1
2
，x∈(0，π)，且f（x）=m有且仅有一个实根，求实数m的值．
已知f（x）=sin(ωx+
π
3
)（ω＞0），f（
π
6
）=f（
π
3
），且f（x）在区间(
π
6
，
π
3
)上有最小值，无最大值，则ω=______．
（1）利用“五点法”画出函数f(x)=sin
1
2
x在长度为一个周期的闭区间的简图
（2）求函数f（x）的单调减区间
（1）函数y=
2
3
sin（
1
2
x-
π
4
）的振幅、周期和频率各是多少？它的图象与正弦曲线有什么关系？
（2）求函数y=tan（
π
2
x+
π
3
）的定义域、周期与单调递增区间．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网