题目内容
设关于x函数 其中0
其中0
将f(x)的最小值m表示成a的函数m=g(a);
是否存在实数a,使f(x)>0在 上恒成立?
上恒成立?
是否存在实数a,使函数f(x) 在 上单调递增?若存在,写出所有的a组成的集合;若不存在,说明理由.
上单调递增?若存在,写出所有的a组成的集合;若不存在,说明理由.
(1)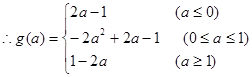 (2)不存在a;(3)
(2)不存在a;(3)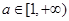 .
.
解析试题分析:(1)先利用二倍角公式将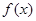 化简
化简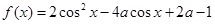 ,将其看成
,将其看成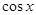 的二次函数,从而转化成求二次函数的最值问题.因为含参数,要注意定义域的范围,对参数进行讨论.
的二次函数,从而转化成求二次函数的最值问题.因为含参数,要注意定义域的范围,对参数进行讨论.
(2)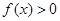 恒成立
恒成立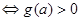 ,即求
,即求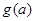 的最大值大于0即可.而
的最大值大于0即可.而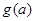 的最大值为
的最大值为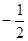 ,所以
,所以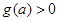 无解.故不存在a,使得
无解.故不存在a,使得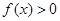 恒成立.
恒成立.
(3)本题可看成二次函数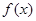 在
在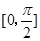 上递增,只需
上递增,只需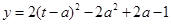 在
在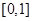 上单调递减,故
上单调递减,故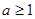 .
.
(1)设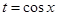 , 由
, 由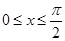 知
知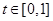 ,
,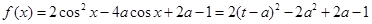
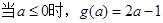
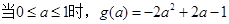
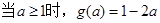
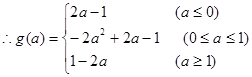
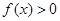 恒成立
恒成立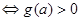
由于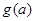 的最大值为
的最大值为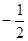 ,所以
,所以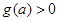 无解.
无解.
故不存在a,使得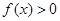 恒成立.
恒成立.
(3)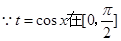 上的减函数,故
上的减函数,故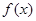 在
在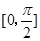 上递增,只需
上递增,只需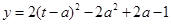 在
在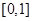 上单调递减,故
上单调递减,故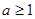
所以存在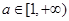 ,使函数
,使函数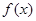 为增函数.
为增函数.
考点:二倍角公式,二次函数的性质,最值,恒成立问题,等价转化的方法,函数的单调性.

练习册系列答案
相关题目
 其中
其中 且
且 .
.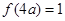 ,求
,求 的值;
的值; 上
上 恒成立,求
恒成立,求
 的最小值;
的最小值; 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,都有
,都有 成立.
成立. 残骸,我国“雪龙号”科考船于2014年3月26日从港口
残骸,我国“雪龙号”科考船于2014年3月26日从港口 出发,沿北偏东
出发,沿北偏东 角的射线
角的射线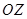 方向航行,而在港口北偏东
方向航行,而在港口北偏东 角的方向上有一个给科考船补给物资的小岛
角的方向上有一个给科考船补给物资的小岛 ,
,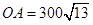 海里,且
海里,且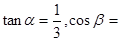
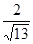 .现指挥部需要紧急征调位于港口
.现指挥部需要紧急征调位于港口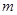 海里的
海里的 处的补给船,速往小岛
处的补给船,速往小岛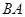 方向全速追赶科考船,并在
方向全速追赶科考船,并在 处相遇.经测算当两船运行的航线与海岸线
处相遇.经测算当两船运行的航线与海岸线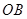 围成的三角形
围成的三角形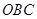 的面积
的面积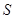 最小时,这种补给方案最优.
最小时,这种补给方案最优.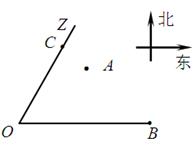
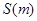 ;
; 为偶函数.
为偶函数. 的值;
的值; 有且只有一个根,求实数
有且只有一个根,求实数 的取值范围.
的取值范围.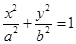 (a>b>0)的离心率为
(a>b>0)的离心率为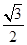 ,过其右焦点F与长轴垂直的弦长为1,
,过其右焦点F与长轴垂直的弦长为1,
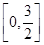 上的最大值.
上的最大值.