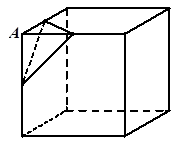题目内容
长方体ABCD—A B
B CD中,
CD中,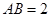 ,
,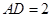 ,
,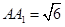 ,则点
,则点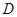 到平面
到平面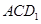 的距离是( )
的距离是( )
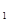 B
B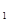 CD中,
CD中,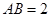 ,
,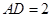 ,
,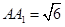 ,则点
,则点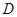 到平面
到平面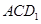 的距离是( )
的距离是( ) A. | B. | C.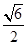 | D.2 |
C
试题分析:因为在长方体ABCD—A
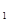 B
B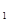 CD中,
CD中,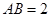 ,
,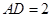 ,
,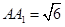 ,可知面对角线
,可知面对角线 ,AC=2
,AC=2 ,CD1=
,CD1= ,则利用
,则利用 ,即
,即 ,故选C
,故选C点评:解决该试题的关键是将点到面的距离的求解转换为等体积法,来求解得到。或者作出调到面的距离,来表示求解。

练习册系列答案
相关题目
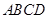 是矩形,
是矩形,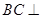 平面
平面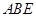 ,
,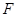 是
是 上一点,
上一点,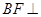 平面
平面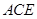 ,点
,点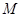 ,
,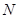 分别是
分别是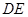 的中点.
的中点. 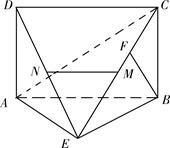
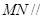 平面
平面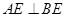 .
.  的各棱长均为2,侧面
的各棱长均为2,侧面
 底面
底面 ,侧棱
,侧棱 与底面
与底面 .
. 与底面
与底面 上是否存在点
上是否存在点 ,使得平面
,使得平面 平面
平面 ?若存在,求出
?若存在,求出 的长;若不存在,请说明理由。
的长;若不存在,请说明理由。
 等于
等于















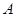 是棱长为
是棱长为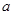 的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:①有
的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:①有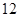 个顶点;②有
个顶点;②有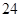 条棱;③有
条棱;③有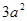 ;⑤体积为
;⑤体积为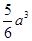 .其中正确的结论是____________.(要求填上所有正确结论的序号)
.其中正确的结论是____________.(要求填上所有正确结论的序号)