题目内容
16.如表是关于某设备的使用年份x和所需要的维修费用y (万元)的几组统计数据:| x(年份) | 2012 | 2013 | 2014 | 2015 | 2016 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(2)估计2020年,该设备维修费用为多少?
分析 (1)先做出两组数据的平均数,把平均数和条件中所给的两组数据代入求解b的公式,做出b的值,再求出a的值,写出回归直线的方程.
(2)把x=2020代入直线的方程得到y=12.38,估计维修的费用.这是一个预报值,不是正确数值
解答 解1:(1)$\bar x$=$\frac{1}{5}$(2012+2013+2014+2015+2016)=2014,
$\bar y$=$\frac{1}{5}$(2.2+3.8+5.5+6.55+7)=5,
$\sum_{i=1}^5{({x_i}-\bar x)({y_i}-\bar y)}=12.3$,$\sum_{i=1}^5{{{({x_i}-\bar x)}^2}}=10$,
∴$\hat b=\frac{{\sum_{i=1}^5{({x_i}-\bar x)({y_i}-\bar y)}}}{{\sum_{i=1}^5{{{({x_i}-\bar x)}^2}}}}=1.23$$\hat a=\bar y-\hat b\overline{x}=-2472.22$,
∴$所求的回归直线方程为\hat y=1.23x-2472.22$
另解:设X=x-2014,Y=y-5.5 则
| X | -2 | -1 | 0 | 1 | 2 |
| Y | -3.3 | -1.7 | 0 | 1 | 1.5 |
∴$\hat b=\frac{{\sum_{i=1}^5{{X_i}{Y_i}-5\bar X\bar Y}}}{{\sum_{i=1}^5{{X^2}_i-5{{\bar X}^2}}}}=\frac{12.3}{10}=1.23$,
$\hat a=\bar Y-\hat b\overline{X}=-0.5$,
∴$\hat Y=1.23X-0.5$,
∴$所求的回归直线方程为\hat y-5.5=1.23(x-2014)-0.5$,
即$\hat y=1.23x-2472.22$…..(8分)
(2)当x=2020时,$\hat y=12.38$(万元)
∴估计2020年,该设备维修费用为12.38万元…..(12分)
点评 本题考查线性回归方程的求解和应用,是一个基础题,解题的关键是正确应用最小二乘法来求线性回归方程的系数.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
4.已知向量$\overrightarrow{a}$=(2,-1),$\overrightarrow{b}$=(1,7),则下列结论正确的是( )
| A. | $\overrightarrow{a}$⊥$\overrightarrow{b}$ | B. | $\overrightarrow{a}$∥$\overrightarrow{b}$ | C. | $\overrightarrow{a}$⊥($\overrightarrow{a}$+$\overrightarrow{b}$) | D. | $\overrightarrow{a}$⊥($\overrightarrow{a}$-$\overrightarrow{b}$) |
5.已知|$\overrightarrow{a}$|=5,|$\overrightarrow{b}$|=4,$\overrightarrow{a}$•$\overrightarrow{b}$=-10,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{5π}{6}$ |
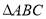 中,“角
中,“角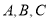 成等差数列”是“
成等差数列”是“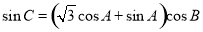 ”的( )
”的( ) 上的偶函数
上的偶函数 在
在 上单调递减,且
上单调递减,且 ,则不等式
,则不等式 的解集是__________.
的解集是__________. 甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取6次.得到甲、乙两位学生成绩的茎叶图.
甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取6次.得到甲、乙两位学生成绩的茎叶图.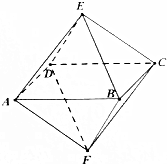 如图,已知一个八面体的各条棱长均为1,四边形ABCD为正方形,给出下列命题:
如图,已知一个八面体的各条棱长均为1,四边形ABCD为正方形,给出下列命题: