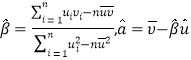题目内容
【题目】如图,已知椭圆![]() 的右焦点为
的右焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,过原点
上,过原点![]() 的直线与椭圆
的直线与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
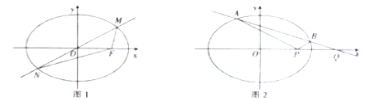
(Ⅱ)设![]() ,
,![]() ,过点
,过点![]() 且斜率不为零的直线与椭圆
且斜率不为零的直线与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,证明:
两点,证明:![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)见解析.
;(Ⅱ)见解析.
【解析】
(Ⅰ)取椭圆![]() 的左焦点
的左焦点![]() ,连
,连![]() 、
、![]() ,由椭圆的几何性质知
,由椭圆的几何性质知![]() ,则
,则![]() ,设椭圆方程代入点
,设椭圆方程代入点![]() 即可求解(Ⅱ)设点
即可求解(Ⅱ)设点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 的方程为:
的方程为:![]() ,联立方程组,消元得
,联立方程组,消元得![]() ,写出
,写出![]() 的斜率,同理得直线
的斜率,同理得直线![]() 的斜率,利用根与系数的关系化简即可得出结论.
的斜率,利用根与系数的关系化简即可得出结论.
(Ⅰ)如图,取椭圆![]() 的左焦点
的左焦点![]() ,连
,连![]() 、
、![]() ,由椭圆的几何性质知
,由椭圆的几何性质知![]() ,则
,则![]() ,得
,得![]() ,
,
将点![]() 代入椭圆
代入椭圆![]() 的方程得:
的方程得:![]() ,解得:
,解得:![]()
故椭圆![]() 的方程为:
的方程为:![]() .
.
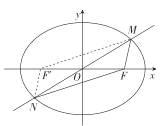
(Ⅱ)设点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]()
由图可知直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为:
的方程为:![]()
联立方程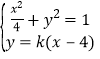 ,消去
,消去![]() 得:
得:![]() ,
,
![]() ,
,![]() .
.
有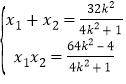
直线![]() 的斜率为:
的斜率为:![]() .
.
同理直线![]() 的斜率为:
的斜率为:![]() .
.
由![]()
![]()
![]()
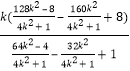
![]()
![]() .
.
由上得直线![]() 与
与![]() 的斜率互为相反数,可得
的斜率互为相反数,可得![]() .
.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目