题目内容
【题目】设集合![]() ,
, ![]() 是集合
是集合![]() 的所有子集组成的集合.若集合
的所有子集组成的集合.若集合![]() 满足对任意的映射
满足对任意的映射![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,其中,
成立,其中,![]() 表示集合
表示集合![]() 的子集
的子集![]() 的补集,
的补集,![]() 为给定的正整数.试求所有满足上述条件的集合
为给定的正整数.试求所有满足上述条件的集合![]() .
.
【答案】见解析
【解析】
记![]() .若存在有限子集
.若存在有限子集![]() ,满足
,满足![]() .
.
首先证明:存在映射![]() ,对任意的集合
,对任意的集合![]() ,均有
,均有![]() .
.
设集合![]() 的全部子集构成的集合为
的全部子集构成的集合为![]() ,
,
其中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
定义映射![]() ,
,![]() ,
,![]() ,则对任意的
,则对任意的![]() ,均有
,均有![]() .
.
定义映射![]() ,对于任意的
,对于任意的![]() ,设
,设![]() ,
,![]() .则
.则![]() .
.
定义
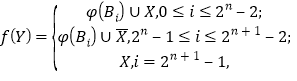
其中,![]() .则对任意的
.则对任意的![]() ,均有
,均有![]() .
.
因此,对于映射![]() ,若不存在集合
,若不存在集合![]() ,使得
,使得![]() ,则
,则![]() .
.
其次证明:对任何有限集![]() ,
,![]() ,均满足题设条件.
,均满足题设条件.
反证法.
假设存在映射![]() ,使得对任意的
,使得对任意的![]() ,均有
,均有![]() .
.
任取![]() ,由
,由![]() 是有限集,故必存在整数
是有限集,故必存在整数![]() ,使得
,使得![]() ,且对任意的
,且对任意的![]() 、
、![]() ,有
,有![]() .
.
设![]() .则
.则![]() .
.
同理,![]() ,
,![]() ,……
,……
![]() .
.
由此知![]() .
.
所以,![]() ,与
,与![]() 不含不为1的奇数因子矛盾.
不含不为1的奇数因子矛盾.
因此,不存在这样的映射![]() ,使得对任意的
,使得对任意的![]() ,均有
,均有![]() ,即对任一映射
,即对任一映射![]() ,均存在
,均存在![]() ,有
,有![]() .
.
从而,![]() 必为所有元素个数小于或等于
必为所有元素个数小于或等于![]() 的实数的集合.
的实数的集合.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目