题目内容
9.若方程ln(k-ex)+x-1=0有解,求k的最小值2$\sqrt{e}$.分析 由方程ln(k-ex)+x-1=0有解,可得k=ex+e1-x,对ex+e1-x,运用基本不等式即可得到所求最小值.
解答 解:ln(k-ex)+x-1=0,
即有ln(k-ex)=1-x,
k-ex=e1-x,
即为k=ex+e1-x,
由ex+e1-x≥2$\sqrt{{e}^{x}•{e}^{1-x}}$=2$\sqrt{e}$,
当且仅当ex=e1-x,即x=$\frac{1}{2}$时,取得等号.
则方程ln(k-ex)+x-1=0有解,
k的最小值为2$\sqrt{e}$,
故答案为:2$\sqrt{e}$.
点评 本题考查方程有解的条件,注意运用分离参数法,考查转化思想和基本不等式的运用:求最值,考查运算能力,属于中档题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 B.
B.
 D.
D.
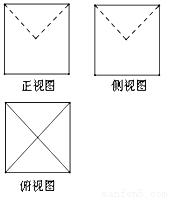
 如图,两个正方形ABCD和ADEF所在平面互相垂直,设M、N分别是BD和AE的中点,那么①AD⊥MN;②MN∥平面CDE;③MN∥CE;④MN、CE异面.其中假命题的个数为( )
如图,两个正方形ABCD和ADEF所在平面互相垂直,设M、N分别是BD和AE的中点,那么①AD⊥MN;②MN∥平面CDE;③MN∥CE;④MN、CE异面.其中假命题的个数为( ) 的首项是
的首项是 ,公差
,公差 ,且
,且 是
是 与
与 的等比中项,则
的等比中项,则 ( )
( ) B.
B.
 D.
D.
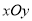 中,直线
中,直线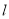 的参数方程为
的参数方程为 (
(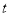 为参数),以原点
为参数),以原点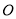 为极点,
为极点,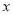 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线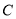 的极坐标方程为
的极坐标方程为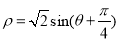 .
.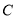 的直角坐标方程;
的直角坐标方程;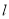 与曲线
与曲线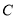 交于
交于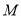 ,
,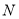 两点,求
两点,求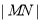 .
. 的首项是
的首项是 ,公差
,公差 ,且
,且 是
是 与
与 的等比中项,则
的等比中项,则 ( )
( ) B.
B.
 D.
D.