题目内容

18．函数f（x）=$\frac{1}{2}$sinx+$\frac{\sqrt{3}}{2}$cosx的最大值是1．

分析 利用两角和的正弦公式化简函数的解析式，再利用正弦函数的值域，求出它的最大值．

解答 解：∵函数f（x）=$\frac{1}{2}$sinx+$\frac{\sqrt{3}}{2}$cosx=sin（x+$\frac{π}{3}$），
故当x+$\frac{π}{3}$=2kπ+$\frac{π}{2}$，即x=2kπ+$\frac{π}{6}$，k∈Z时，
函数f（x）取得最大值为1，
故答案为：1．

点评 本题主要考查两角和的正弦公式，正弦函数的值域，属于基础题．

练习册系列答案
相关题目
10．已知α，β是两个不同的平面，m，n是两条不同的直线，给出下列命题：
①若m⊥α，m?β，则α⊥β；
②若m⊥n，m⊥α，则n∥α；
③若m?α，n?β，α∥β，则m∥n；
④若m∥α，α⊥β，则m⊥β．
其中，正确的个数是（　　）
A．0B．1C．2D．3
10．已知函数f（x）=$\frac{1}{xsinθ}$+lnx在[1，+∞）上为增函数，且θ∈（0，π）．
（Ⅰ）求函数f（x）在其定义域内的极值；
（Ⅱ）若在[1，e]上至少存在一个x0，使得kx0-f（x0）＞$\frac{2e}{{x}_{0}}$成立，求实数k的取值范围．
6．给出以下命题，其中正确命题的序号是①④（把你认为正确的序号都填上）
①非零向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$|+|$\overrightarrow{b}$|，则存在实数t，使得$\overrightarrow{b}$=t$\overrightarrow{a}$成立；
②若数列{an}是等差数列，且am+an=as+at（m、n、s、t∈N*），则m+n=s+t；
③若Sn是等比数列{an}的前n项和，则S6，S12-S6，S18-S12成等比数列；
④在△ABC中，若$\frac{1}{tanA}$，$\frac{1}{tanB}$，$\frac{1}{tanC}$依次成等差数列，则a2，b2，c2依次成等差数列．
13．某市统计局就本地居民的月收入调查了10000人，并根据所得数据画了样本的频率分布直方图（每个分组包括左端点，不包括右短点，如第一组表示月收入在[1000，1500）（单位：元）

（Ⅰ）估计居民月收入在[1500，2000）的概率
（Ⅱ）根据频率分布直方图估计样本数据的众数、中位数
（Ⅲ）统计方法中．同一组数据常用该组区间的中点值作为代表，据此估计样本数据的平均数．
2．若函数f（x）=|2x-2|-b有两个零点，则实数b的取值范围是（　　）
A．（-2，0）B．（-1，0）C．（0，1）D．（0，2）
9．若方程ln（k-ex）+x-1=0有解，求k的最小值2$\sqrt{e}$．

如图，在四棱锥中，底面是边长为1的正方形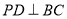，，，且，为的中点．

（1）求证：平面；

（2）求直线与平面所成角的正弦值．
2．两条直线l1：mx-4y+2=0与12：4x+5y+n=0互相垂直，交于点A（2，p），求n+p-m的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网