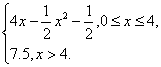题目内容
某厂生产某种产品x(百台),总成本为C(x)(万元),其中固定成本为2万元,每生产1百台,成本增加1万元,销售收入R(x)=
(万元),假定该产品产销平衡.
(1)若要该厂不亏本,产量x应控制在什么范围内?
(2)该厂年产多少台时,可使利润最大?
(3)求该厂利润最大时产品的售价.
|
(1)若要该厂不亏本,产量x应控制在什么范围内?
(2)该厂年产多少台时,可使利润最大?
(3)求该厂利润最大时产品的售价.
分析:由题意写出成本函数,则收入函数减去成本函数即可得到利润函数.
(1)由利润函数大于等于0,分段求解x的取值范围,取并集得答案;
(2)分段求解利润函数的最大值,取各段最大值中的最大者;
(3)(2)中求出了利润最大时的x的值,把求得的x值代入
得答案.
(1)由利润函数大于等于0,分段求解x的取值范围,取并集得答案;
(2)分段求解利润函数的最大值,取各段最大值中的最大者;
(3)(2)中求出了利润最大时的x的值,把求得的x值代入
| R(x) |
| x |
解答:解:由题意得,成本函数为C(x)=2+x,
从而利润函数L(x)=R(x)-C(x)=
.
(1)要使不亏本,只要L(x)≥0,
当0≤x≤4时,L(x)≥0⇒3x-0.5x2-2.5≥0⇒1≤x≤4,
当x>4时,L(x)≥0⇒5.5-x≥0⇒4<x≤5.5.
综上,1≤x≤5.5.
答:若要该厂不亏本,产量x应控制在100台到550台之间.
(2)当0≤x≤4时,L(x)=-0.5(x-3)2+2,
故当x=2时,L(x)max=2(万元),
当x>4时,L(x)<1.5<2.
综上,当年产300台时,可使利润最大.
(3)由(2)知x=3,时,利润最大,此时的售价为P=
=2.33(万元/百台)=233元/台.
从而利润函数L(x)=R(x)-C(x)=
|
(1)要使不亏本,只要L(x)≥0,
当0≤x≤4时,L(x)≥0⇒3x-0.5x2-2.5≥0⇒1≤x≤4,
当x>4时,L(x)≥0⇒5.5-x≥0⇒4<x≤5.5.
综上,1≤x≤5.5.
答:若要该厂不亏本,产量x应控制在100台到550台之间.
(2)当0≤x≤4时,L(x)=-0.5(x-3)2+2,
故当x=2时,L(x)max=2(万元),
当x>4时,L(x)<1.5<2.
综上,当年产300台时,可使利润最大.
(3)由(2)知x=3,时,利润最大,此时的售价为P=
| R(3) |
| 3 |
点评:本题考查了函数模型的选择与应用,考查了简单的数学建模思想方法,训练了分段函数的最值得求法,分段函数的最值要分段求,该题属中档题.

练习册系列答案
 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目