题目内容
已知函数f(x)＝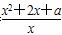
，x∈[1，＋∞)．
(1)当a＝4时，求f(x)的最小值；
(2)当a＝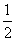
时，求f(x)的最小值；
(3)若a为正常数，求f(x)的最小值．
[解析] (1)当a＝4时，f(x)＝x＋
＋2，易知f(x)在[1,2]上是减少的，在[2，＋∞)上是增加的．
∴f(x)min＝f(2)＝6.
(2)当a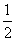＝时，f(x)＝x＋
＋2，易知f(x)在[1，＋∞)上为增加的，∴f(x)min＝f(1)＝
.
(3)函数f(x)＝x＋
＋2在(0，
]上是减少的，
在[，＋∞)上是增加的．
若>1，即a>1时，f(x)在区间[1，＋ ∞)上先减后增，f(x)min＝f()＝2＋2；
若≤1，即0<a≤1时，f(x)在区间 [1，＋∞)上是增加的．
∴f(x)min＝f(1)＝a＋3.
综上所述，f(x)min＝
.
练习册系列答案
名校课堂系列答案
相关题目
在区间[0,4]上的最大值M与最小值N的和为________．
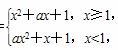则“－2≤a≤0”是“函数f(x)在R上单调递增”的( )
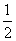)＝0，则不等式f(log4x)>0的解集是________．