题目内容
下面几种推理是类比推理的是( )
| A、两条直线平行,同旁内角互补,如果∠A和∠B是两条平行直线的同旁内角,则∠A+∠B=180° |
| B、由平面向量的运算性质,推测空间向量的运算性质 |
| C、某校高二级有20个班,1班有51位团员,2班有53位团员,3班有52位团员,由此可以推测各班都超过50位团员 |
| D、一切偶数都能被2整除,2100是偶数,所以2100能被2整除 |
考点:类比推理
专题:探究型,推理和证明
分析:本题考查的知识点是类比推理的定义,根据归纳推理、类比推理和演绎推理的定义,对答案中的四个推理进行判断,即可得到答案.
解答:
解:A中,两条直线平行,同旁内角互补,如果∠A和∠B是两条平行直线的同旁内角,则∠A+∠B=180°为演绎推理;
B中,由平面向量的运算性质,推测空间向量的运算性质,为类比推理;
C中,某校高二级有20个班,1班有51位团员,2班有53位团员,3班有52位团员,由此可以推测各班都超过50位团员,为归纳推理;
D中,一切偶数都能被2整除,.2100是偶数,所以2100能被2整除,为演绎推理;
故选:B.
B中,由平面向量的运算性质,推测空间向量的运算性质,为类比推理;
C中,某校高二级有20个班,1班有51位团员,2班有53位团员,3班有52位团员,由此可以推测各班都超过50位团员,为归纳推理;
D中,一切偶数都能被2整除,.2100是偶数,所以2100能被2整除,为演绎推理;
故选:B.
点评:本题考查的知识点是类比推理,熟练掌握归纳推理、类比推理和演绎推理的定义,是解答本题的关键.

练习册系列答案
相关题目
i是虚数单位,复数z=1+
在复平面内对应的点位于( )
| 1 |
| i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
cos(-240°)的值为( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
命题p:直线ax+by+c=0与圆x2+y2=1恰有一个公共点,命题q:a,b,c为直角三角形的三条边,则p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
下表是某厂1到4月份用水量情况(单位:百吨)的一组数据:
用水量y与月份x之间具有线性相关关系,其线性回归方程为
=-0.7x+a,则a的值为( )
| 月份x | 1 | 2 | 3 | 4 |
| 用水量ym3 | 4.5 | 4 | 3 | 2.5 |
| ∧ |
| y |
| A、5.25 | B、5 |
| C、2.5 | D、3.5 |
某学校高一年级有35个班,每个班有56名同学都是从1到56编的号码.为了交流学习经验,要求每班号码为14的同学留下进行交流,这里运用的是( )
| A、分层抽样 | B、抽签抽样 |
| C、随机抽样 | D、系统抽样 |
已知函数f(x)=
,则f(lg2+lg5)=( )
|
| A、10 | B、1 | C、0 | D、-1 |
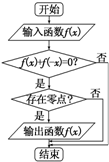 某流程图如图所示,现输入如下四个函数
某流程图如图所示,现输入如下四个函数