Question

已知空间四面体O-ABC，点P满足

OP

=

1

6

OA

+

1

3

OB

+

1

2

OC

，记四面体O-ABP、O-BCP、O-ACP的体积依次为V₁，V₂，V₃，则V₁：V₂：V₃=

 

．

Answer 1

考点：棱柱、棱锥、棱台的体积

专题：综合题,空间位置关系与距离

分析：点P满足

OP

=

1

6

OA

+

1

3

OB

+

1

2

OC

，可得P，A，B，C四点共面，

PA

+2

PB

+3

PC

=

0

，进而确定P到BC的距离等于A到BC的距离的

1

6

，P到AC的距离等于B到AC的距离的

1

3

．从而，S₃ =

1

3

S．∴S₁ =S-S₂-S₃ =

1

2

S，从而求得S₁：S₂：S₃ 的值，即可求出V₁：V₂：V₃．

解答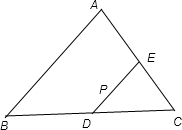： 解：记△ABP、△BCP、△ACP的面积依次为S₁、S₂、S₃．
∵点P满足

OP

=

1

6

OA

+

1

3

OB

+

1

2

OC

，
∴P，A，B，C四点共面，

PA

+2

PB

+3

PC

=

0

设D、E 分别为BC、AC的中点，∴

PA

-

PB

=-3（

PB

+

PC

），
∴

BA

=-3×2

PD

=-6

PD

，
同理由（

PA

+

PC

）=-2（

PB

+

PC

），即2

PE

=-2×

PD

，
∴

PE

=-

1

3

BA

．∴P到BC的距离等于A到BC的距离的

1

6

，
设△ABC的面积为S，则S₂ =

1

6

S．
 P到AC的距离等于B到AC的距离的

1

3

，
∴S₃ =

1

3

S．∴S₁ =S-S₂-S₃ =

1

2

S．
∴S₁：S₂：S₃ =3：1：2，
∴V₁：V₂：V₃=3：1：2．
故答案为：3：1：2．

点评：本题考查共线向量的意义，两个同底的三角形的面积之比等于底上的高之比，体现了数形结合的数学思想．