题目内容
已知两同心圆的半径分别是5和4，AB为小圆的一条直径．
(1)求以大圆的切线为准线，且过A、B两点的抛物线的焦点的轨迹M；
(2)设过轨迹M的中心的弦为PQ，F是轨迹M的焦点，求S△PQF的最大值．
答案：
解析：
解析：
|
(1)建立如图所示的直角坐标系，则A(－4，0)、B(4，0)，设N为大圆上的任一点，l为过N点的大圆的切线，并设抛物线的焦点为F(x，y)，作AA1⊥l于A1，BB1⊥l于B1，由抛物线的定义得|AF|＝|AA1|，|BF|＝|BB1|．
所以|AF|＋|BF|＝|AA1|＋|BB1|＝2|OO1|＝10，而A，B为定点，故焦点F的轨迹M是以A，B为焦点，长轴长为10，焦距为8的椭圆(除去长轴上的两个端点)，其方程为 (2)根据椭圆的对称性，有S△PQF＝2S△OFP，设△OFP的边OF上的高为h，则 S△QFP＝2× 因为h≤3，所以当h＝3时，S△QFP的最大面积是12． |
＋
＝1(y≠0)．
|OF|h＝4h
练习册系列答案
名校课堂系列答案
相关题目
如图，已知|AB|=10，图中的一系列圆是圆心分别为A、B的两组同心圆，每组同心圆的半径分别是1，2，3，…，n，…．利用这两组同心圆可以画出以A、B为焦点的双曲线．若其中经过点M、N、P的双曲线的离心率分别是eM，eN，eP．则它们的大小关系是
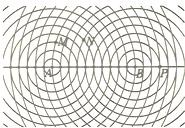如图，已知|AB|=10，图中的一系列圆是圆心分别A，B的两组同心圆，每组同心圆的半径分别是1，2，3，…，n，利用这两组同心圆可以画出以A，B为焦点的椭圆，设其中经过点M，N，P的椭圆的离心率分别是eM，eN，eP，则（ ）| A、eM=eN=eP | B、eP＜eM=eN | C、eM＜eN＜eP | D、eP＜eM＜eN |
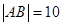，图中的一系列圆是圆心分别为A、B的两组同心圆，每组同心圆的半径分别是1，2，3，…，n，….利用这两组同心圆可以画出以A、B为焦点的双曲线. 若其中经过点M、N、P的双曲线的离心率分别是
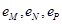.则它们的大小关系是
（用“
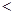”连接）.
