题目内容
已知函数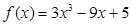 .
.
(Ⅰ)求函数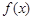 的单调递增区间;
的单调递增区间;
(Ⅱ)求函数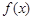 在
在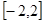 的最大值和最小值.
的最大值和最小值.
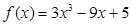 .
.(Ⅰ)求函数
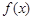 的单调递增区间;
的单调递增区间;(Ⅱ)求函数
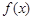 在
在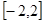 的最大值和最小值.
的最大值和最小值.(1)
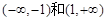
(2)函数
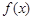 取得最小值
取得最小值 .函数
.函数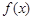 取得最大值11.
取得最大值11.本试题主要是考查了导数来判定函数的单调区间,并能求解函数给定闭区间的最值问题。基本题型,需要熟练掌握。
解:(1)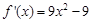 . 令
. 令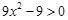 ,
,
解此不等式,得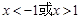 .
.
因此,函数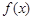 的单调增区间为
的单调增区间为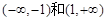 .
.
(2) 令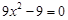 ,得
,得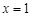 或
或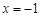 .
.
当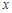 变化时,
变化时,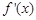 ,
,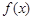 变化状态如下表:
变化状态如下表:
从表中可以看出,当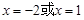 时,函数
时,函数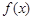 取得最小值
取得最小值 .
.
当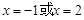 时,函数
时,函数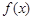 取得最大值11.
取得最大值11.
解:(1)
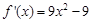 . 令
. 令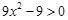 ,
, 解此不等式,得
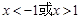 .
. 因此,函数
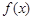 的单调增区间为
的单调增区间为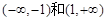 .
. (2) 令
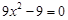 ,得
,得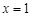 或
或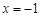 .
.当
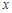 变化时,
变化时,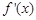 ,
,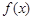 变化状态如下表:
变化状态如下表: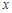 | -2 | 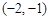 | -1 |  | 1 | 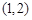 | 2 |
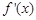 | 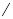 | + | 0 | - | 0 | + | 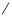 |
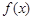 | -1 |  | 11 | 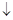 | -1 |  | 11 |
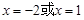 时,函数
时,函数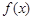 取得最小值
取得最小值 .
.当
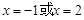 时,函数
时,函数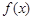 取得最大值11.
取得最大值11.
练习册系列答案
相关题目
 ,已知
,已知 在
在 时取得极值,则
时取得极值,则 =( )
=( ) 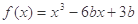 在
在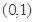 内有极小值,求实数
内有极小值,求实数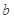 的取值范围是
的取值范围是 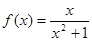
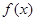 的极大值和极小值,并画出函数
的极大值和极小值,并画出函数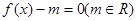 的根的个数问题:
的根的个数问题: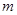 的取值范围
的取值范围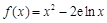 .(
.(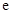 为自然对数的底)
为自然对数的底)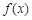 的最小值;
的最小值;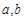 使得
使得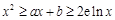 对于任意的正数
对于任意的正数 恒成立?若存在,求出
恒成立?若存在,求出 在
在 处取极值
处取极值 ,则
,则 =( )
=( )


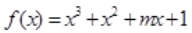 在R上无极值点,则实数m的取值范围是____.
在R上无极值点,则实数m的取值范围是____. 在
在 处有极值,则
处有极值,则



 函数
函数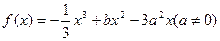 在
在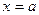 处取得极值.
处取得极值.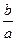 ;
;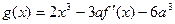 ,如果
,如果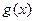 在开区间
在开区间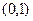 上存在极小值,求实数
上存在极小值,求实数 的取值范围.
的取值范围.