题目内容

函数y=sin（2x-
π
3
）在区间[-
π
2
，π]的简图是（　　）
A、
B、
C、
D、
考点：正弦函数的图象
专题：三角函数的图像与性质
分析：根据函数解析式可得当x=-
π
2
时，y=sin[（2×(-
π
2
)-
π
3
]＞0，故排除A，D；当x=
π
6
时，y=sin0=0，故排除C，从而得解．
解答： 解：当x=-
π
2
时，y=sin[（2×(-
π
2
)-
π
3
]=-sin（π+
π
3
）=sin
π
3
=
3
2
＞0，故排除A，D；
当x=
π
6
时，y=sin（2×
π
6
-
π
3
）=sin0=0，故排除C；
故选：B．
点评：本题主要考查了正弦函数的图象和性质，属于基础题．
练习册系列答案
相关题目
设数列{an}的前n项和为Sn，对任意的正整数n，都有an=5Sn+1成立．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设bn=log4|an|，求数列{
1
bn•bn+1
}前n项和Tn．
一篮球运动员投篮的命中率为60%，以η表示他首次投中时累计已投篮的次数，则η的数学期望是
 
．
一口袋中装有5个白球和3个红球，这些球除颜色外完全相同．现从袋中往外取球，每次任取一个记下颜色后放回，直到红球出现10次时停止，设停止时共取了ξ次球，则P（ξ=12）=
 
．（用式子作答）
若x＞0，y＞0，则“x2+y2＞1”是“x+y＞1”的（　　）
A、必要不充分条件
B、充分不必要条件
C、充要条件
D、既不充分也不必要条件
已知
a
=（2sin（x+
θ
2
），
3
），
b
=（cos（x+
θ
2
），2cos2（x+
θ
2
）），f（x）=
a
•
b
-
3
．
（1）求f（x）的解析式
（2）若0＜θ＜π，求θ使f（x）为偶函数，并求此时f（x）=1，x∈[-π，π]的角的集合．
求：sin220°+cos280°+
3
sin20°cos80°的值．
方程ln（2x+1）=
1
3x+2
的一个根落在区间（　　）（参考数值：ln1.5≈0.41，ln2≈0.69，ln2.5≈0.92）
A、（-
1
4
，0）
B、（0，
1
4
）
C、（
1
4
，
1
2
）
D、（
1
2
，
3
4
）
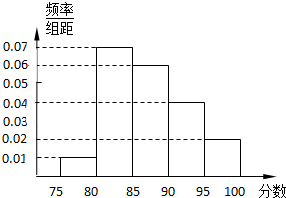某高中进行高中生歌唱比赛，在所有参赛成绩中随机抽取100名学生的成绩，按成绩分组：第1组[75，80），第2组[80，85），第3组[85，90），第4组[90，95），第5组[95，100]得到的频率分布直方图如图所示．现在组委会决定在笔试成绩高的第3，4，5组中用分层抽样抽取6名学生进入第二轮面试．
（1）求3，4，5组各应该抽取多少人进入第二轮面试；
（2）学校决定在（1）中抽取的这6名学生中随机抽取2名学生接受考官D的面试，设第3组中有ξ名学生被考官D面试，求ξ的分布列和数学期望．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网