题目内容
定义在R上的任意函数f (x)都可以表示成一个奇函数g (x)和一个偶函数h (x)之和,如果f (x)=lg(10x+1),x∈R.那么
| A.g (x)=x,h (x)=lg(10x+10-x+1) |
B.g (x)= ,h (x)= ,h (x)= |
C.g (x)= ,h (x)=lg(10x+1)- ,h (x)=lg(10x+1)- |
D.g (x)=- ,h (x)= ,h (x)= |
C.
解析试题分析:由题意可知,f(x)=g(x)+h(x)=lg(10x+1)……………………①,
∴g(-x)+h(-x)= lg(10-x+1),即-g(x)+h(x)= lg(10-x+1)…………②
①②联立可得,h(x)= lg(10x+1)- ,g (x)=
,g (x)= 。故答案为C。
。故答案为C。
考点:本题考查函数奇偶性的灵活应用。
点评:本题的关键是f(x)=g(x)+h(x),然后以-x代入x,再利用奇偶性进行化简建立方程组求解.

练习册系列答案
相关题目
已知: 在
在 上为减函数,则
上为减函数,则 的取值范围为( )。
的取值范围为( )。
A. | B. | C. | D. |
函数 在区间
在区间 上递减,则实数
上递减,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D.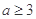 |
函数 的图像恒过定点
的图像恒过定点 ,若点
,若点 在直线
在直线 上,其中
上,其中 ,则
,则 的最小值为( )
的最小值为( )
| A.1 | B.2 | C.3 | D.4 |
已知常数 且
且 ,则函数
,则函数 恒过定点
恒过定点
A. | B. | C. | D. |
若a>0,a≠1,且m>0,n>0,则下列各式中正确的是 ( )
| A.logam•logan=loga(m+n) | B.am•an=am•n |
C. | D. |
下列各组函数中的两个函数是相等函数的是( )
A. |
B. |
C. |
D. |
若幂函数
 的图象过点
的图象过点 ,则
,则 为
为
A. | B. | C.1 | D.2 |
偶函数  在
在  上单调递增,则
上单调递增,则  与
与 的大小关系是 ( )
的大小关系是 ( )
A. | B. |
C. | D. |