题目内容
满足
，下列不等式中正确的是（ ）
A． | B． | C． | D． |
C
解析试题分析：因为，而函数
单调递增，所以.
考点：本小题主要考查幂函数的单调性的应用.
点评：幂函数的单调性与指数有关，指数大于零，在
上单调递增；指数小于零，在上单调递减.
练习册系列答案
相关题目
若函数
的定义域都是R，则
成立的充要条件是（ ）
A．有一个 ，使 | B．有无数多个，使 |
C．对R中任意的x，使 | D．在R中不存在x，使 |
当
时，
（
）,则
的取值范围是( )
A．（０， ） | B．（，１） | C．（１， ） | D．（，２） |
已知
，若方程
存在三个不等的实根
，则
的取值范围是
A． | B． | C． | D． |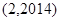
设函数
的值域为R，则常数
的取值范围是
A． | B． | C． | D． |
函数y=(2k+1)x+b在(-∞,+∞)上是减函数，则（ ）
A．k> | B．k< | C．k> | D．k< |
的零点个数是（ ）
| A．0个 | B．1个 | C．2个 | D．3个 |
函数
的实数解落在的区间是( )
A． | B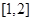． | C． | D． |
已知：
在
上为减函数，则
的取值范围为（ ）。
A． | B． | C． | D． |