题目内容
函数
在
上恒为正数，则实数
的取值范围是（ ）
A． | B． | C． | D． |
C
解析试题分析：设
，由题意可知
且
时
，结合二次函数的单调性可得
综上
考点：函数单调性及最值
点评：本题结合函数图象分析考虑
练习册系列答案
口算题天天练系列答案
相关题目
设函数
的值域为R，则常数
的取值范围是
A． | B． | C． | D． |
已知
，则
的值为( )
| A．－7 | B．3 | C．－8 | D．1 |
不等式
对
恒成立，则
的取值范围是（ ）
A． | B． | C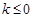． | D． |
已知函数
，则
（ ）
| A．16 | B．8 | C．－8 | D．8或－8 |
已知：
在
上为减函数，则
的取值范围为（ ）。
A． | B． | C． | D． |
已知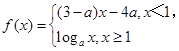
是（-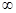
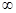，+）上的增函数，那么
的取值范围是( )
| A．(1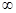， +) | B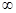．(-,3) | C．[ ，3) | D．(1,3) |
实数
的大小关系正确的是
A． | B． |
C． | D． |
已知常数
且
，则函数
恒过定点
A． | B． | C． | D． |