题目内容
数列{an}满足 .当an取得最大值时n等于
.当an取得最大值时n等于
- A.4
- B.5
- C.6
- D.7
B
分析:根据题意可求得n-1时数列满足的等式,和题设中的等式想减即可求得( )nan =n,进而求得an,则可求得an-an-1,发现当1≤n≤5时结果大于0,n≥5时结果小于0,进而根据数列的单调性可推断出n=5时数列的值最大.
)nan =n,进而求得an,则可求得an-an-1,发现当1≤n≤5时结果大于0,n≥5时结果小于0,进而根据数列的单调性可推断出n=5时数列的值最大.
解答: a1=
a1= (12+1)
(12+1)
a1=
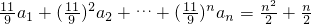
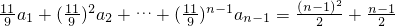
两式想减可得( )nan =n
)nan =n
∴an=n•( )n
)n
∴an-an-1=n•( )n-(n-1)•(
)n-(n-1)•( )n-1=
)n-1=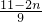 •(
•( )n
)n
∴1≤n≤5时an-an-1>0,数列成递增趋势,n≥5时an-an-1<0,数列成递减趋势,
∴n=5时an最大
故选B.
点评:本题主要考查了数列的求和,解题的关键是利用了数列的单调性来确定数列的最大值.
分析:根据题意可求得n-1时数列满足的等式,和题设中的等式想减即可求得(
 )nan =n,进而求得an,则可求得an-an-1,发现当1≤n≤5时结果大于0,n≥5时结果小于0,进而根据数列的单调性可推断出n=5时数列的值最大.
)nan =n,进而求得an,则可求得an-an-1,发现当1≤n≤5时结果大于0,n≥5时结果小于0,进而根据数列的单调性可推断出n=5时数列的值最大.解答:
 a1=
a1= (12+1)
(12+1) a1=

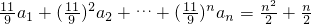
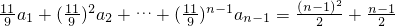
两式想减可得(
 )nan =n
)nan =n∴an=n•(
 )n
)n∴an-an-1=n•(
 )n-(n-1)•(
)n-(n-1)•( )n-1=
)n-1=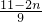 •(
•( )n
)n∴1≤n≤5时an-an-1>0,数列成递增趋势,n≥5时an-an-1<0,数列成递减趋势,
∴n=5时an最大
故选B.
点评:本题主要考查了数列的求和,解题的关键是利用了数列的单调性来确定数列的最大值.

练习册系列答案
相关题目

 ,当t<a1<t+1(其中t>2)时有an+k=an(k∈N*),则k的最小值为( )
,当t<a1<t+1(其中t>2)时有an+k=an(k∈N*),则k的最小值为( ) .当an取得最大值时n等于( )
.当an取得最大值时n等于( )