题目内容
【题目】已知函数![]() .
.
(1)求不等式![]() 的解集;
的解集;
(2)若直线![]() 与
与![]() 的图象所围成的多边形面积为
的图象所围成的多边形面积为![]() ,求实数
,求实数![]() 的值.
的值.
【答案】(1) ![]() (2)4
(2)4
【解析】
(Ⅰ)去掉绝对值号,得到分段函数,分类讨论即可求解不等式的解集,得到答案;
(Ⅱ)画出函数![]() 的图象,得出直线
的图象,得出直线![]() 与函数
与函数![]() 围成的图形,利用梯形的面积公式,即可求解.
围成的图形,利用梯形的面积公式,即可求解.
(Ⅰ)由题意,可得函数f(x)=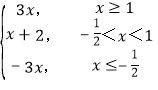 ,
,
由f(x)≥3可知:
(i)当x≥1时,3x≥3,即x≥1;
(ii)当-![]() <x<1时,x+2>3,即x≥1,与-
<x<1时,x+2>3,即x≥1,与-![]() <x<1矛盾,舍去;
<x<1矛盾,舍去;
(iii)当x≤-![]() 时,-3x≥3,即x≤-1;
时,-3x≥3,即x≤-1;
综上可知解集为{x|x≤-1或x≥1}.
(Ⅱ)画出函数y=f(x)的图象,如图所示,其中A(-![]() ,
,![]() ),B(1,3),
),B(1,3),
由kAB=1,知y=x+a图象与直线AB平行,若要围成多边形,则a>2.
易得y=x+a与y=f(x)图象交于两点C(![]() ,
,![]() ),D(-
),D(-![]() ,
,![]() ),则|CD|=
),则|CD|=![]() |
|![]() +
+![]() |=
|=![]() a.
a.
平行线AB与Cd间的距离d=![]() =
=![]() ,且|AB|=
,且|AB|=![]() ,
,
∴梯形ABCD的面积S=![]()
![]() =
=![]() (a-2)=
(a-2)=![]() ,(a>2).
,(a>2).
即(a+2-(a-2)=12,∴a=4,
故所求实数a的值为4.
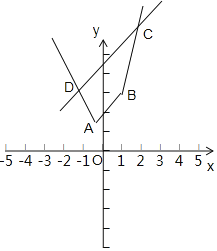

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目