题目内容
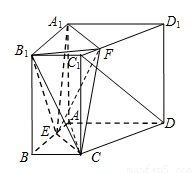
(本小题满分14分)如图,在四棱柱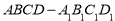 中,
中,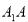
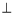 底面
底面 ,
,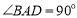 ,
,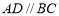 ,且
,且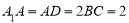 ,
, . 点E在棱AB上,平面
. 点E在棱AB上,平面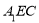 与棱
与棱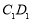 相交于点F.
相交于点F.
(Ⅰ)求证: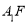 ∥平面
∥平面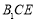 ;
;
(Ⅱ)求证: 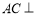 平面
平面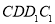 ;
;
(Ⅲ)写出三棱锥 体积的取值范围. (结论不要求证明)
体积的取值范围. (结论不要求证明)
(Ⅰ)详见解析; (Ⅱ)详见解析;(Ⅲ)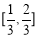 .
.
【解析】
试题分析:(Ⅰ)因为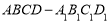 是棱柱,所以平面
是棱柱,所以平面 平面
平面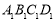 .由面面平行的性质定理,可得
.由面面平行的性质定理,可得 ∥
∥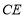 ,再根据线面平行的判定定理即可证明结论;(Ⅱ)在四边形ABCD中,因为
,再根据线面平行的判定定理即可证明结论;(Ⅱ)在四边形ABCD中,因为 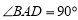 ,
, ,且
,且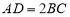 ,
,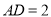 ,
,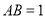 ,利用勾股定理可得,
,利用勾股定理可得, 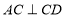 ,又
,又 .又
.又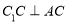 ,根据面面垂直的判定定理即可证明结果;(Ⅲ)由题意可知,三棱锥
,根据面面垂直的判定定理即可证明结果;(Ⅲ)由题意可知,三棱锥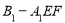 的体积的取值范围是
的体积的取值范围是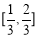 .
.
试题解析:(Ⅰ)证明:因为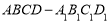 是棱柱,
是棱柱,
所以平面 平面
平面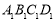 .
.
又因为平面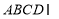 平面
平面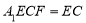 ,
,
平面 平面
平面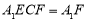 ,
,
所以  ∥
∥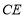 . 3分
. 3分
又 
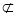 平面
平面 ,
,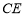
 平面
平面 ,
,
所以 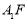 ∥平面
∥平面 . 6分
. 6分
(Ⅱ)证明:在四边形ABCD中,
因为 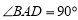 ,
, ,且
,且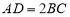 ,
,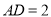 ,
,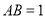 ,
,
所以 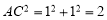 ,
,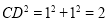 .
.
所以  ,
,
所以 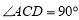 ,即
,即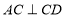 . 7分
. 7分
因为 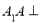 平面
平面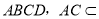 平面
平面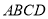 ,
,
所以  .
.
因为在四棱柱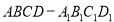 中,
中, ,
,
所以 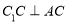 . 9分
. 9分
又因为 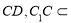 平面
平面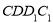 ,
, ,
,
所以 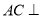 平面
平面 . 11分
. 11分
(Ⅲ)【解析】
三棱锥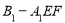 的体积的取值范围是
的体积的取值范围是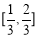 . 14分.
. 14分.
考点:1.线面平行的判定定理和性质定理;2.线面垂直的判定定理;3.锥体的体积公式.

练习册系列答案
相关题目
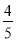 ,自然科学课程的概率都是
,自然科学课程的概率都是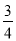 ,且各门课程通过与否相互独立.用
,且各门课程通过与否相互独立.用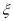 表示该同学所选的3门课程通过的门数,求随机变量
表示该同学所选的3门课程通过的门数,求随机变量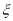 的概率分布列和数学期望。
的概率分布列和数学期望。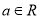 ,则“
,则“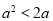 ”是“
”是“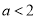 ”成立的( )
”成立的( )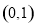 上单调递减的函数为( ).
上单调递减的函数为( ).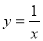 B.
B. C.
C.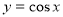 D.
D.
 为双曲线C:
为双曲线C: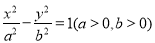 的左、右焦点,且直线
的左、右焦点,且直线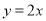 为双曲线C的一条渐近线,点P为C上一点,如果
为双曲线C的一条渐近线,点P为C上一点,如果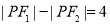 ,那么双曲线C的方程为____;离心率为_____.
,那么双曲线C的方程为____;离心率为_____.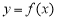 的定义域为
的定义域为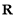 ,则“
,则“ ”是“函数
”是“函数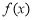 为奇函数”的( )
为奇函数”的( ) 表示的平面区域,点
表示的平面区域,点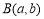 为坐标平面
为坐标平面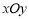 内一点,若对于区域D内的任一点
内一点,若对于区域D内的任一点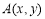 ,都有
,都有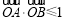 成立,则
成立,则 的最大值等于( )
的最大值等于( ) 的各项和等于公比
的各项和等于公比 ,则首项
,则首项 的取值范围是 .
的取值范围是 .