题目内容
(本小题满分10分)某校开设8门校本课程,其中4门课程为人文科学,4门为自然科学,学校要求学生在高中三年内从中选修3门课程,假设学生选修每门课程的机会均等.
(1)求某同学至少选修1门自然科学课程的概率;
(2)已知某同学所选修的3门课程中有1门人文科学,2门自然科学,若该同学通过人文科学课程的概率都是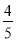 ,自然科学课程的概率都是
,自然科学课程的概率都是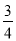 ,且各门课程通过与否相互独立.用
,且各门课程通过与否相互独立.用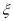 表示该同学所选的3门课程通过的门数,求随机变量
表示该同学所选的3门课程通过的门数,求随机变量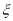 的概率分布列和数学期望。
的概率分布列和数学期望。
(1) ,(2)
,(2) 的分布列为
的分布列为
|
|
|
|
|
|
|
|
|
|

【解析】
试题分析:(1)先求“某同学至少选修1门自然科学课程”对立事件概率: ,从而所求概率为
,从而所求概率为 (2)随机变量
(2)随机变量 的所有可能取值有
的所有可能取值有 .
. ,
, ,
, ,
, ,
,
试题解析:(1)记“某同学至少选修1门自然科学课程”为事件A,
则 , 2分
, 2分
所以该同学至少选修1门自然科学课程的概率为 . 3分
. 3分
(2)随机变量 的所有可能取值有
的所有可能取值有 . 4分
. 4分
因为 ,
,
 ,
,
 ,
,
 , 8分
, 8分
所以 的分布列为
的分布列为
|
|
|
|
|
|
|
|
|
|
所以 . 10分
. 10分
考点:概率分布列和数学期望

练习册系列答案
相关题目









 ,函数
,函数 .
. 的单调递增区间;
的单调递增区间; 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 ,
, ,
, ,求
,求 的面积.
的面积. ,
, ,
, ,则
,则 ,
, ,
, 的大小关系为( )
的大小关系为( ) B.
B. C.
C. D.
D.
 的图象分别向左、向右各平移
的图象分别向左、向右各平移 个单位长度后,所得的两个图象对称轴重合,则
个单位长度后,所得的两个图象对称轴重合,则  的最小值为______.
的最小值为______.
 ,求函数
,求函数 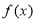 的单调递减区间;
的单调递减区间; 恒成立,求整数 a的最小值:
恒成立,求整数 a的最小值: ,正实数
,正实数  满足
满足  ,证明:
,证明: 
 ,则不等式
,则不等式  的解集为______.
的解集为______.
 .
. 的值;
的值; ,
, ,求丙高中学校中的女生比男生人数多的概率.
,求丙高中学校中的女生比男生人数多的概率.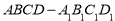 中,
中,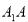
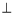 底面
底面 ,
,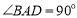 ,
,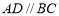 ,且
,且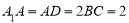 ,
, . 点E在棱AB上,平面
. 点E在棱AB上,平面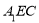 与棱
与棱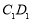 相交于点F.
相交于点F.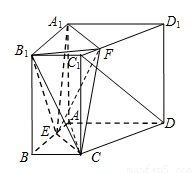
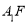 ∥平面
∥平面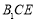 ;
; 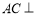 平面
平面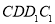 ;
; 体积的取值范围. (结论不要求证明)
体积的取值范围. (结论不要求证明)