题目内容
3．10001000（2）转化为八进制数是210（8）．分析 根据二进制转化为八进制的方法，我们从右往左把二进制数每三位分成一段，然后把每一段的数转化为对应的八进制数即可得到结果．
解答 解：10001000（2）=10 001 000（2）=210（8），
故答案为：210（8）
点评 本题考查的知识点是不同进制数之间的转换，解答的关键是熟练掌握不同进制之间数的转化规则．
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
13．已知O为坐标原点，$\overrightarrow{OA}$=（1，2），$\overrightarrow{OB}$=（-2，-1），则$\frac{|\overrightarrow{AB}|}{\overrightarrow{OA}•\overrightarrow{OB}}$=（ ）
| A． | -$\frac{3\sqrt{2}}{2}$ | B． | $\frac{3\sqrt{2}}{2}$ | C． | -$\frac{3\sqrt{2}}{4}$ | D． | $\frac{3\sqrt{2}}{4}$ |
8．与向量$\overrightarrow{a}$=（1，3，-2）平行的一个向量的坐标是（ ）
| A． | （$\frac{1}{3}$，1，1） | B． | （-$\frac{1}{2}$，-$\frac{3}{2}$，1） | C． | （-$\frac{1}{2}$，$\frac{3}{2}$，-1） | D． | （$\sqrt{2}$，-3，-2$\sqrt{2}$） |
15．曲线y=x3+sinx在点O（0，0）处切线方程是（ ）
| A． | y=x | B． | y=2x | C． | y=3x | D． | y=4x |
12．
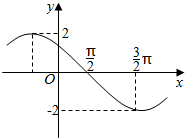已知f（x）=Asin（ωx+φ），（A＞0，ω＞0，0＜φ＜π）的图象的一部分如图所示，则f（x）解析式是（ ）
已知f（x）=Asin（ωx+φ），（A＞0，ω＞0，0＜φ＜π）的图象的一部分如图所示，则f（x）解析式是（ ）| A． | f（x）=2sin（$\frac{1}{2}$x-$\frac{π}{4}$） | B． | f（x）=2sin（$\frac{1}{2}$x+$\frac{3π}{4}$） | C． | f（x）=2sin（2x-$\frac{π}{4}$） | D． | f（x）=2sin（2x+$\frac{3π}{4}$） |
13．函数$y=cos（-x）cos（\frac{π}{2}-x）$的最小正周期是（ ）
| A． | $\frac{π}{2}$ | B． | π | C． | $\frac{3π}{2}$ | D． | 2π |