题目内容
如果对定义在R上的函数 ,对任意两个不相等的实数
,对任意两个不相等的实数 都有
都有 ,则称函数
,则称函数 为“H函数”.
为“H函数”.
给出下列函数:
① ;
;
② ;
;
③ ;
;
④ .
.
以上函数是“H函数”的所有序号为__________(把所有正确命题的序号都填上).
②③
【解析】
试题分析:因为对定义在R上的函数 ,对任意两个不相等的实数
,对任意两个不相等的实数 都有
都有 ,即
,即 恒成立即函数
恒成立即函数 是定义在
是定义在 上是增函数,①
上是增函数,① 在
在 上不单调,不满足条件;②
上不单调,不满足条件;② 在
在 上是增函数;③
上是增函数;③ ,
, 在
在 上是增函数;④
上是增函数;④ ,当
,当 时,函数单调递增,当
时,函数单调递增,当 时,在是减函数不满足条件,所以函数是“H函数”的所有序号为②③
时,在是减函数不满足条件,所以函数是“H函数”的所有序号为②③
考点:函数的单调性的应用

练习册系列答案
相关题目
 }定义如下:
}定义如下: =1,当
=1,当 时,
时, ,若
,若 ,则
,则 的值等于( )
的值等于( ) 在复平面内对应的点的坐标为( )
在复平面内对应的点的坐标为( ) B.
B. C.
C. D.
D.
 的图象可能是
的图象可能是
 的离心率为
的离心率为 ,右焦点
,右焦点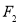 到直线
到直线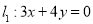 的距离为
的距离为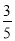 .
.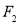 斜率为
斜率为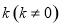 的直线
的直线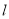 与椭圆C相交于E、F两点,A为椭圆的右顶点,直线AE,AF分别交直线
与椭圆C相交于E、F两点,A为椭圆的右顶点,直线AE,AF分别交直线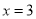 于点M,N,线段MN的中点为P,记直线
于点M,N,线段MN的中点为P,记直线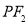 的斜率为
的斜率为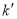 ,求证:
,求证: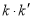 为定值.
为定值. 是自然对数的底数,函数
是自然对数的底数,函数 的零点为
的零点为 ,函数
,函数 的零点为b,则下列不等式成立的是
的零点为b,则下列不等式成立的是



 ,命题“若
,命题“若 ,则
,则 ”的否命题是
”的否命题是



 的解集记为
的解集记为 ,若
,若 则 ( )
则 ( ) B.
B.
 D.
D.
 ,若
,若 对
对 恒成立,则
恒成立,则 的取值范围为 .
的取值范围为 .