题目内容
(本小题满分13分)已知椭圆 的离心率为
的离心率为 ,右焦点
,右焦点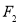 到直线
到直线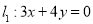 的距离为
的距离为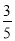 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过椭圆右焦点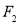 斜率为
斜率为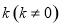 的直线
的直线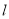 与椭圆C相交于E、F两点,A为椭圆的右顶点,直线AE,AF分别交直线
与椭圆C相交于E、F两点,A为椭圆的右顶点,直线AE,AF分别交直线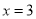 于点M,N,线段MN的中点为P,记直线
于点M,N,线段MN的中点为P,记直线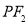 的斜率为
的斜率为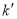 ,求证:
,求证: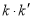 为定值.
为定值.
(Ⅰ) (Ⅱ)
(Ⅱ)
【解析】
试题分析:(1)根据离心率为 ,可得
,可得 之间的关系,再右焦点
之间的关系,再右焦点 到直线
到直线 的距离为
的距离为 ,就可求出
,就可求出 的值,从而求出
的值,从而求出 的值(2)解决直线和椭圆的综合问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与椭圆的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式
的值(2)解决直线和椭圆的综合问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与椭圆的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式 :计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论.
:计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论.
试题解析:(Ⅰ)由题意得 ,
, , 2分
, 2分
所以 ,
, ,所求椭圆方程为
,所求椭圆方程为 . 4分
. 4分
(Ⅱ)设过点 的直线
的直线 方程为:
方程为: ,
,
设点 ,点
,点 , 5分
, 5分
将直线 方程
方程 代入椭圆
代入椭圆 ,
,
整理得: 6分
6分
因为点 在椭圆内,所以直线
在椭圆内,所以直线 和椭圆都相交,
和椭圆都相交, 恒成立,
恒成立,
且
 7分
7分
直线 的方程为:
的方程为: ,直线
,直线 的方程为:
的方程为:
令 ,得点
,得点 ,
, ,所以点
,所以点 的坐标
的坐标 ,
,
9分
直线 的斜率为
的斜率为
 , 11分
, 11分
将 代入上式得:
代入上式得:
 ,
,
所以 为定值
为定值 . 13
. 13
考点:(1)椭圆的方程;(2)直线与椭圆的综合问题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
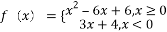 ,若互不相等的实数
,若互不相等的实数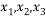 满足
满足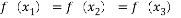 ,则
,则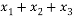 的取值范围是( )
的取值范围是( )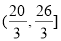 B.
B.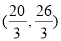 C.
C. D.
D.
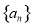 为等比数列,且
为等比数列,且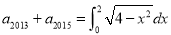 ,则
,则 的值为( )
的值为( )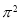 B.
B.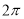 C.
C.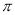 D.
D.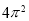
 上随机选取一个数X,则
上随机选取一个数X,则 的概率等于__________.
的概率等于__________. 的值为2,则输出的
的值为2,则输出的 的值为
的值为
 ,对任意两个不相等的实数
,对任意两个不相等的实数 都有
都有 ,则称函数
,则称函数 为“H函数”.
为“H函数”. ;
; ;
; ;
; .
.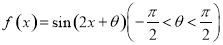 的图象向右平移
的图象向右平移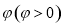 个单位长度后得到函数
个单位长度后得到函数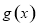 的图象,若
的图象,若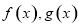 的图象都经过点
的图象都经过点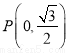 ,则
,则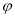 的值可以是
的值可以是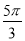 B.
B.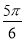 C.
C.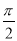 D.
D.
 在
在 内有定义,下列函数:
内有定义,下列函数: ;
;  ;
;  ;
; 中必为奇函数的有 .
中必为奇函数的有 .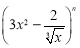
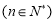 展开式中含有常数项,则
展开式中含有常数项,则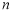 的最小取值是
的最小取值是