题目内容
如图,三棱柱ABC-A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90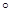 ,BC=1,AC=CC1=2.
,BC=1,AC=CC1=2.
(1)证明:AC1⊥A1B;
(2)设直线AA1与平面BCC1B1的距离为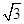 ,求二面角A1-AB-C的大小.
,求二面角A1-AB-C的大小.
(1)证明详见解析;(2)arctan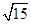 .
.
解析试题分析:(1)利用AC1⊥平面ABC,可得平面AA1C1C⊥平面ABC,在利用平面与平面垂直的性质和已知条件可得BC⊥平面AA1C1C,而AC1⊥A1C,所以AC1⊥A1B.
(2)作A1E⊥C1C,E为垂足,则A1E⊥平面BCC1B1,而直线A A1∥平面BCC1B1,A1E为直线A A1与平面BCC1B1间的距离,则A1D=A1E=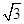 ,然后证明∠A1FD为二面角A1-AB-C的平面角,求出tan∠A1FD=
,然后证明∠A1FD为二面角A1-AB-C的平面角,求出tan∠A1FD= 即可.
即可.
试题解析:
解法一:(1)∵A1D⊥平面ABC, A1D 平面AA1C1C,故平面AA1C1C⊥平面ABC,又BC⊥AC,所以BC⊥平面AA1C1C,连结A1C,因为侧面AA1C1C是棱形,所以AC1⊥A1C,由三垂线定理的AC1⊥A1B.
平面AA1C1C,故平面AA1C1C⊥平面ABC,又BC⊥AC,所以BC⊥平面AA1C1C,连结A1C,因为侧面AA1C1C是棱形,所以AC1⊥A1C,由三垂线定理的AC1⊥A1B.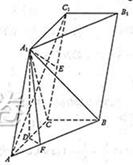
(2) BC⊥平面AA1C1C,BC 平面BCC1B1,故平面AA1C1C⊥平面BCC1B1,
平面BCC1B1,故平面AA1C1C⊥平面BCC1B1,
作A1E⊥C1C,E为垂足,则A1E⊥平面BCC1B1,又直线A A1∥平面BCC1B1,因而A1E为直线A A1与平面BCC1B1间的距离,A1E=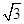 ,因为A1C为∠ACC1的平分线,故A1D=A1E=
,因为A1C为∠ACC1的平分线,故A1D=A1E=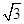 ,
,
作DF⊥AB,F为垂足,连结A1F,由三垂线定理得A1F⊥AB,故∠A1FD为二面角A1-AB-C的平面角,由AD=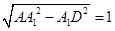 ,得D为AC的中点,DF=
,得D为AC的中点,DF=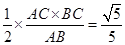 ,tan∠A1FD=
,tan∠A1FD= ,所以二面角A1-AB-C的大小为arctan
,所以二面角A1-AB-C的大小为arctan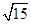 .
.
解法二:以C为坐标原点,射线CA为x轴的正半轴,以CB的长为单位长,建立如图所示的空间直角坐标系C-xyz,由题设知A1D与z轴平行,z轴在平面AA1C1C内.
(1)设A1(a,0,c),由题设有a≤2,A(2,0,0)B(0,1,0),则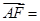 (-2,1,0),
(-2,1,0),
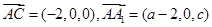 ,
,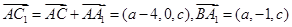 ,由
,由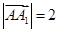 得
得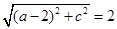 ,即
,即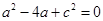 ,于是
,于是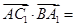
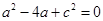 ①,所以
①,所以 .
.
(2)设平面BCC1B1的法向量 ,则
,则 ,
, ,即
,即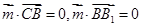 ,因
,因 ,故y=0,且(a-2)x-cz=0,令x=c,则z=2-a,
,故y=0,且(a-2)x-cz=0,令x=c,则z=2-a, ,点A到平面BCC1B1的距离为
,点A到平面BCC1B1的距离为 ,又依题设,点A到平面BCC1B1的距离为
,又依题设,点A到平面BCC1B1的距离为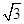 ,所以c=
,所以c= 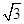 .代入①得a=3(舍去)或a=1.于是
.代入①得a=3(舍去)或a=1.于是 ,
,
设平面ABA1的法向量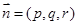 ,则
,则 ,即
,即 .
. 且-2p+q=0,令p=
且-2p+q=0,令p=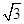 ,则q=2
,则q=2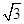 ,r=1,
,r=1, ,又
,又 为平面ABC的法向量,故cos
为平面ABC的法向量,故cos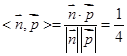 ,所以二面角A1-AB-C的大小为arccos
,所以二面角A1-AB-C的大小为arccos ,
,
考点:1.直线与平面垂直的判断和性质;2.二面角的求法;3.平面与平面垂直的判断和性质.

 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
 的高为
的高为 ,底面
,底面 是边长为
是边长为 的正方形,顶点
的正方形,顶点 在底面上的射影是正方形
在底面上的射影是正方形 .
. 是棱
是棱 的中点.试求直线
的中点.试求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,
中, 为矩形,平面
为矩形,平面 平面
平面

 问
问 为何值时,四棱锥
为何值时,四棱锥 与平面
与平面 夹角的余弦值.
夹角的余弦值.

 .
. 平面
平面 .
.
 中,
中, ,
, 为
为 的中点,
的中点, 为
为 的中点.
的中点. 平面
平面 ;
; 平面
平面 ;
; 为正方体
为正方体 的点
的点 的个数,并说明理由.
的个数,并说明理由.
 为互不重合的平面,W#W$W%.K**S*&5^U
为互不重合的平面,W#W$W%.K**S*&5^U 是互不重合的直线,给出下列四个命题:
是互不重合的直线,给出下列四个命题: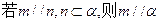
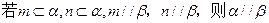
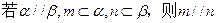
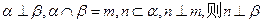 ;
;