题目内容
如图,在正方体 中,
中, ,
, 为
为 的中点,
的中点, 为
为 的中点.
的中点.
(1)求证:平面 平面
平面 ;
;
(2)求证: 平面
平面 ;
;
(3)设 为正方体
为正方体 棱上一点,给出满足条件
棱上一点,给出满足条件 的点
的点 的个数,并说明理由.
的个数,并说明理由.
(1)详见解析;(2)详见解析;(3)在正方体 棱上使得
棱上使得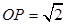 的点
的点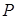 有12个.
有12个.
解析试题分析:(1)求证:平面 平面
平面 ,证明两平面垂直,只需证明一个平面过另一个平面的垂线,注意到本题是一个正方体,因此可证
,证明两平面垂直,只需证明一个平面过另一个平面的垂线,注意到本题是一个正方体,因此可证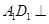 平面
平面 即可;(2)求证:
即可;(2)求证: 平面
平面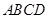 ,证明线面平行,即证线线平行,即在平面
,证明线面平行,即证线线平行,即在平面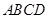 内找一条直线与
内找一条直线与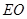 平行,注意到
平行,注意到 为
为 的中点,
的中点, 为
为 的中点,可连接
的中点,可连接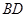 ,
,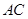 ,设
,设 ,连接
,连接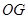 ,证明
,证明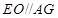 即可,即证四边形
即可,即证四边形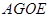 是平行四边形即可;(3)设
是平行四边形即可;(3)设 为正方体
为正方体 棱上一点,给出满足条件
棱上一点,给出满足条件 的点
的点 的个数,由(2)可知,
的个数,由(2)可知,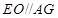 ,且
,且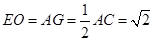 ,故点
,故点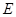 符合,有正方体的特征,可知,
符合,有正方体的特征,可知,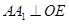 ,故
,故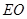 是点
是点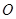 到
到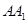 的最短距离,故这样的点就一个,同理在其他棱上各有一个,故可求出满足条件
的最短距离,故这样的点就一个,同理在其他棱上各有一个,故可求出满足条件 的点
的点 的个数.
的个数.
(1)在正方体 中,
中,
因为 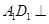 平面
平面 ,
,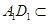 平面
平面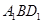 ,
,
所以平面 平面
平面 . 4分
. 4分
(2)证明:连接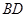 ,
,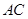 ,设
,设 ,连接
,连接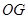 .
.
因为 为正方体,
为正方体,
所以 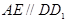 ,且
,且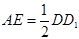 ,且
,且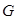 是
是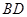 的中点,
的中点,
又因为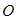 是
是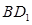 的中点,
的中点,
所以 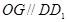 ,且
,且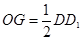 ,
,
所以 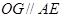 ,且
,且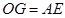 ,
,
即四边形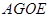 是平行四边形,
是平行四边形,
所以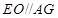 , 6分
, 6分
又因为 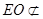 平面
平面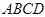 ,
,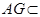 平面
平面 ,
,
所以  平面
平面
练习册系列答案
相关题目
 ,BC=1,AC=CC1=2.
,BC=1,AC=CC1=2.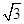 ,求二面角A1-AB-C的大小.
,求二面角A1-AB-C的大小.
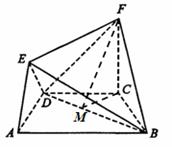

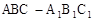 中,
中,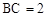 ,
,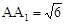 ,D、E分别是
,D、E分别是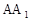 、
、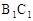 的中点,
的中点,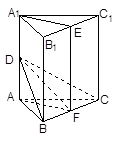
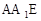 ⊥面BCD;
⊥面BCD;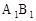 与平面BCD所成的角.
与平面BCD所成的角. 中,
中, ,
, ,点
,点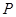 为
为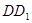 的中点。
的中点。
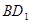 ∥平面
∥平面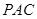 ;
;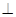 平面
平面 ;
;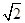 .
.
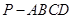 中,
中,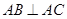 ,
,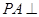 平面
平面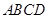 ,且
,且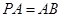 ,点
,点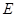 是
是 的中点.
的中点.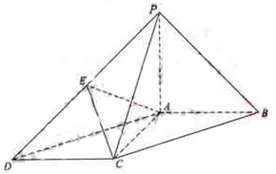
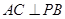 ;
;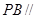 平面
平面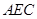 ;
;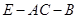 的大小.
的大小.