题目内容
(本小题满分12分)
如图,四棱锥 中,
中, 为矩形,平面
为矩形,平面 平面
平面 .
.
求证:

若 问
问 为何值时,四棱锥
为何值时,四棱锥 的体积最大?并求此时平面
的体积最大?并求此时平面 与平面
与平面 夹角的余弦值.
夹角的余弦值.
(1)详见解析,(2)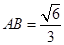 时,四棱锥的体积P-ABCD最大. 平面BPC与平面DPC夹角的余弦值为
时,四棱锥的体积P-ABCD最大. 平面BPC与平面DPC夹角的余弦值为
解析试题分析:(1)先将面面垂直转化为线面垂直:ABCD为矩形,故AB AD,又平面PAD
AD,又平面PAD 平面ABCD,平面PAD
平面ABCD,平面PAD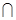 平面ABCD=AD,所以AB
平面ABCD=AD,所以AB 平面PAD,再根据线面垂直证线线垂直:因为PD
平面PAD,再根据线面垂直证线线垂直:因为PD 平面PAD,所以AB
平面PAD,所以AB PD
PD
(2)求四棱锥体积,关键要作出高.这可利用面面垂直性质定理:过P作AD的垂线,垂足为O,又平面PAD 平面ABCD,平面PAD
平面ABCD,平面PAD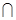 平面ABCD=AD,所以PO
平面ABCD=AD,所以PO 平面ABCD,下面用
平面ABCD,下面用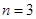 表示高及底面积:设
表示高及底面积:设 ,则
,则 ,故四棱锥P-ABCD的体积为
,故四棱锥P-ABCD的体积为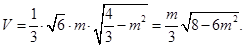 故当
故当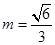 时,即
时,即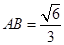 时,四棱锥的体积P-ABCD最大.
时,四棱锥的体积P-ABCD最大.
求二面角的余弦值,可利用空间向量求解,根据题意可建立空间坐标系,分别求出平面BPC的法向量及
平面DPC的法向量,再利用向量数量积求夹角余弦值即可.
试题解析:(1)证明:ABCD为矩形,故AB AD,
AD,
又平面PAD 平面ABCD
平面ABCD
平面PAD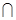 平面ABCD=AD
平面ABCD=AD
所以AB 平面PAD,因为PD
平面PAD,因为PD 平面PAD,故AB
平面PAD,故AB PD
PD
(2)解:过P作AD的垂线,垂足为O,过O作BC的垂线,垂足为G,连接PG.
故PO 平面ABCD,BC
平面ABCD,BC 平面POG,BC
平面POG,BC PG
PG
在直角三角形BPC中,
设 ,则
,则 ,故四棱锥P-ABCD的体积为
,故四棱锥P-ABCD的体积为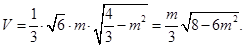
因为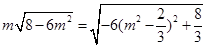
故当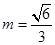 时,即
时,即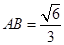 时,四棱锥的体积P-ABCD最大.
时,四棱锥的体积P-ABCD最大.
建立如图所示的空间直角坐标系,
故
设平面BPC的法向量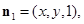 ,则由
,则由 ,
, 得
得
解得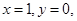
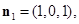
同理可求出平面DPC的法向量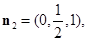 ,从而平面BPC与平面DPC夹角
,从而平面BPC与平面DPC夹角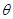 的余弦值为
的余弦值为
考点:面面垂直性质定理,四棱锥体积,利用空间向量求二面角

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 -A BC中,AB
-A BC中,AB  AC, AB=AC=2,
AC, AB=AC=2, =4,点D是BC的中点.
=4,点D是BC的中点. 与
与 所成角的余弦值;
所成角的余弦值; 与
与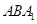 所成二面角的正弦值.
所成二面角的正弦值.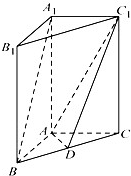
 ,BC=,求二面角S-AB-C的余弦值.
,BC=,求二面角S-AB-C的余弦值.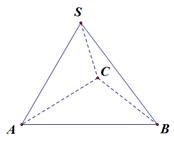
 中,点
中,点 分别是棱
分别是棱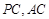 的中点.
的中点.  //平面
//平面 ;
; 平面
平面 ,
, ,求证:
,求证: .
.
 ,BC=1,AC=CC1=2.
,BC=1,AC=CC1=2.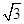 ,求二面角A1-AB-C的大小.
,求二面角A1-AB-C的大小.
 ,
, 为圆柱
为圆柱 的母线,
的母线, 是底面圆
是底面圆 的直径,
的直径,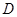 ,
,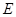 分别是
分别是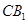 的中点,
的中点,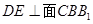 .
. ;
; ;
; 内会有被捕的危险,求鱼被捕的概率.
内会有被捕的危险,求鱼被捕的概率.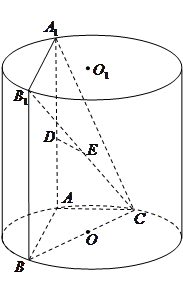

 与平面
与平面 相交,直线
相交,直线 是平面
是平面 ,则直线
,则直线