Question

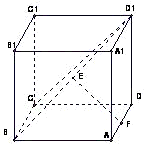已知长方体ABCD-A₁B₁C₁D₁中，A₁A=AB，E、F分别是BD₁和AD中点．
（1）求异面直线CD₁、EF所成的角；
（2）证明EF是异面直线AD和BD₁的公垂线．

Answer 1

解：（1）∵在平行四边形BAD₁C₁中，
E也是AC₁的中点，∴EF∥C₁D，（2分）
∴两相交直线D₁C与CD₁所成的角即异面直线CD₁与EF所成的角．（4分）
又A₁A=AB，长方体的侧面ABB₁A₁，
CDD₁C₁都是正方形，∴D₁C⊥CD₁
∴异面直线CD₁、EF所成的角为90°．（7分）

（2）证：设AB=AA₁=a，∵D₁F=，
∴EF⊥BD₁．（9分）
由平行四边形BAD₁C₁，知E也是AC₁的中点，
且点E是长方体ABCD-A₁B₁C₁D₁的对称中心，（12分）
∴EA=ED，∴EF⊥AD，又EF⊥BD₁，
∴EF是异面直线BD₁与AD的公垂线．（14分）
分析：（1）根据题意，易得EF∥C₁D，即直线D₁C与CD₁所成的角即异面直线CD₁与EF所成的角，计算可得答案；
（2）AB=AA₁=a，D₁F=可得EF⊥BD₁，由平行四边形BAD₁C₁，知E也是AC₁的中点且点E是长方体ABCD-A₁B₁C₁D₁的对称中心?EA=ED?EF⊥AD，再由公垂线定义得证．
点评：本题主要考查异面直线所成角的求解过程以及公垂线的证明．