题目内容
已知集合A={x|-4＜x＜2}，B={x|x＜-5或x＞1}，C={x|m-1＜x＜m+1}，m∈R．
（1）求A∩B；
（2）若A∩B⊆C，求实数m的取值范围．
（1）求A∩B；
（2）若A∩B⊆C，求实数m的取值范围．
考点：集合的包含关系判断及应用
专题：计算题,集合
分析：（1）利用交集运算的定义，可求A∩B；
（2）利用（1）的结论，结合A∩B⊆C，求实数m的取值范围．
（2）利用（1）的结论，结合A∩B⊆C，求实数m的取值范围．
解答：
解：（1）A∩B={x|1＜x＜2}（4分）
（2）因为A∩B⊆C
所以
（8分）
即1≤m≤2（10分）
（2）因为A∩B⊆C
所以
|
即1≤m≤2（10分）
点评：本题考查集合的运算与关系，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
如果a＞b，给出下列不等式：（1）
＜
；（2）a3＞b3；（3）a2+1＞b2+1；（4）2a＞2b．其中成立的不等式有（ ）
| 1 |
| a |
| 1 |
| b |
| A、（3）（4） |
| B、（2）（3） |
| C、（2）（4） |
| D、（1）（3） |
在四棱锥P-ABCD中，侧面PCD⊥底面ABCD，PD⊥CD，底面ABCD是直角梯形，AB∥CD，∠ADC=90°，AB=AD=PD=1，CD=2．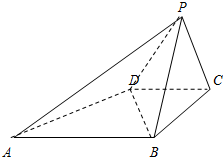
如图，已知四棱锥P-ABCD的底面是直角梯形，∠ABC=∠BCD=90°，