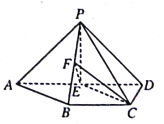
题目内容
【题目】已知点![]() 、
、![]() 为双曲线
为双曲线![]() 的左、右焦点,过
的左、右焦点,过![]() 作垂直于
作垂直于![]() 轴的直线,在
轴的直线,在![]() 轴上方交双曲线
轴上方交双曲线![]() 于点
于点![]() ,且
,且![]() .
.

(1)求双曲线![]() 的两条渐近线的夹角
的两条渐近线的夹角![]() ;
;
(2)过点![]() 的直线
的直线![]() 和双曲线
和双曲线![]() 的右支交于
的右支交于![]() 、
、![]() 两点,求
两点,求![]() 的面积的最小值;
的面积的最小值;
(3)过双曲线![]() 上任意一点
上任意一点![]() 分别作该双曲线两条渐近线的平行线,它们分别交两条渐近线于
分别作该双曲线两条渐近线的平行线,它们分别交两条渐近线于![]() 、
、![]() 两点,求平行四边形
两点,求平行四边形![]() 的面积.
的面积.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)首先根据双曲线的定义,结合题中所给的角的大小,求得![]() ,从而求得b的值,进而得到双曲线的渐近线方程,利用直线的方向向量所成的角,求得两条渐近线的夹角余弦值,利用反余弦求出结果;
,从而求得b的值,进而得到双曲线的渐近线方程,利用直线的方向向量所成的角,求得两条渐近线的夹角余弦值,利用反余弦求出结果;
(2)设出直线的方程,与双曲线的方程联立,利用三角形的面积公式,结合函数的单调性,求得最值,得到结果;
(3)根据所学的知识将四边形的面积表示出来,进而求得结果.
(1)由题意,得![]() ,
,
![]() ,
,
∴![]() ,∴双曲线
,∴双曲线![]() 的方程为
的方程为![]() ,
,
∴![]() ,∴
,∴![]() ;
;
(2)【注:若设点斜式,需补上斜率不存在的情况】
设![]() ,
,![]() 、
、![]() ,
,
将直线![]() 的方程代入双曲线方程,消去
的方程代入双曲线方程,消去![]() ,得
,得![]() ,
,
则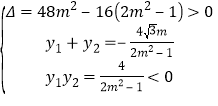 ,得
,得![]() ,
,
![]() ,
,
令![]() ,
,![]() ,则
,则![]() ,
,
其中![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() 在
在![]() 上单调递增,
上单调递增,
∴当![]() 时,
时,![]() 取得最小值
取得最小值![]() ,此时
,此时![]() ,
,![]() 的方程为
的方程为![]() ;
;
(3)设![]() ,其中
,其中![]()
方法一:设![]() ,与
,与![]() 联立,
联立,
可求出![]() ,
,
由三阶行列式表示的三角形面积公式
可得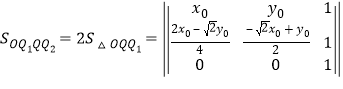
![]() .
.
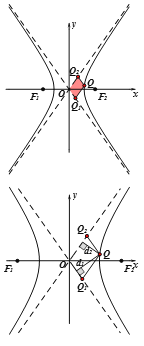
方法二:如图,![]() ,
,![]()
设![]() 到
到![]() 和
和![]() 的距离为
的距离为![]() 、
、![]() ,
,
则![]() ,
,![]() ,
,
∴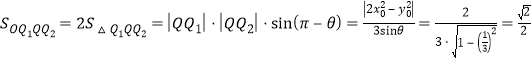

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目