题目内容
已知椭圆C: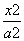 +
+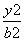 =1(a>b>0)的两个焦点分别为F1(-1,0),F2(1,0),且椭圆C经过点P
=1(a>b>0)的两个焦点分别为F1(-1,0),F2(1,0),且椭圆C经过点P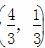 .
.
(1)求椭圆C的离心率;
(2)设过点A(0,2)的直线l与椭圆C交于M,N两点,点Q是线段MN上的点,且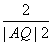 =
=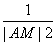 +
+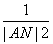 ,求点Q的轨迹方程.
,求点Q的轨迹方程.
解 (1)由椭圆定义知
2a=|PF1|+|PF2|=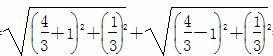 =2
=2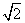 .
.
所以a=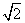 .
.
又由已知得,c=1,所以椭圆C的离心率e=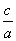 =
=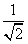 =
=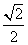 .
.
(2)由(1)知,椭圆C的方程为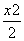 +y2=1.
+y2=1.
设点Q的坐标为(x,y).
(i)当直线l与x轴垂直时,直线l与椭圆C交于(0,1),(0,-1)两点,此时点Q的坐标为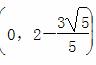 .
.
(ii)当直线l与x轴不垂直时,设直线l的方程为y=kx+2.
因为M,N在直线l上,可设点M,N的坐标分别为(x1,kx1+2),(x2,kx2+2),则
|AM|2=(1+k2)x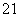 ,|AN|2=(1+k2)x
,|AN|2=(1+k2)x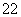 .
.
又|AQ|2=x2+(y-2)2=(1+k2)x2.
由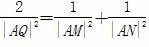 得
得
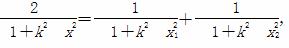 即
即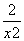 =
=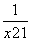 +
+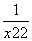 =
=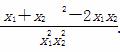 .①
.①
将y=kx+2代入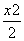 +y2=1中,得
+y2=1中,得
(2k2+1)x2+8kx+6=0.②
由Δ=(8k)2-4×(2k2+1)×6>0,得k2>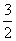 .
.
由②可知,x1+x2=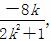 ,x1x2=
,x1x2=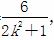 ,
,
代入①中并化简,得
x2=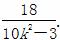 .③
.③
因为点Q在直线y=kx+2上,所以k=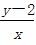 ,代入③中并化简,得10(y-2)2-3x2=18.
,代入③中并化简,得10(y-2)2-3x2=18.
由③及k2>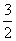 ,可知0<x2<
,可知0<x2<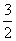 ,
,
即x∈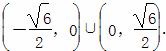
又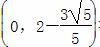 满足10(y-2)2-3x2=18,
满足10(y-2)2-3x2=18,
故x∈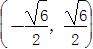 .
.
由题意知点Q(x,y)在椭圆C内,所以-1≤y≤1,
又由10(y-2)2=18+3x2有
(y-2)2∈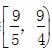 ,且-1≤y≤1,则y∈
,且-1≤y≤1,则y∈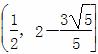 .
.
所以点Q的轨迹方程为10(y-2)2-3x2=18,其中x∈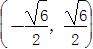 ,y∈
,y∈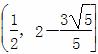 .
.

练习册系列答案
相关题目
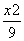 -
-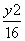 =1的左焦点,P,Q为C上的点.若PQ的长等于虚轴长的2倍,点A(5,0)在线段PQ上,则△ PQF的周长为________.
=1的左焦点,P,Q为C上的点.若PQ的长等于虚轴长的2倍,点A(5,0)在线段PQ上,则△ PQF的周长为________. =0,则P点的轨迹是( ).
=0,则P点的轨迹是( ).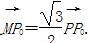
 -
- =1(a>0)的焦点为(5,0),则该双曲线的离心率等于( ).
=1(a>0)的焦点为(5,0),则该双曲线的离心率等于( ). B.
B.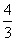 C.
C. D.
D.
 .若AB=4,BC=
.若AB=4,BC= ,则Γ的两个焦点之间的距离为________.
,则Γ的两个焦点之间的距离为________. 则
则 ( )
( )  B、
B、 C、
C、 D、
D、