题目内容
(本小题满分7分)
已知函数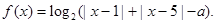
(Ⅰ)当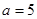 时,求函数
时,求函数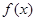 的定义域;
的定义域;
(Ⅱ)当函数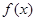 的定义域为R时,求实数
的定义域为R时,求实数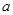 的取值范围。
的取值范围。
已知函数
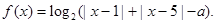
(Ⅰ)当
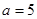 时,求函数
时,求函数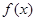 的定义域;
的定义域;(Ⅱ)当函数
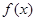 的定义域为R时,求实数
的定义域为R时,求实数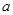 的取值范围。
的取值范围。(1) .(2)
.(2)
 .(2)
.(2)
试题分析:解:(Ⅰ)当
 时,要使函数
时,要使函数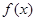 有意义,
有意义,有不等式
 成立,------------------①
成立,------------------① 当
 时,不等式①等价于
时,不等式①等价于 ,即
,即 ,∴
,∴ ;
;当
 时,不等式①等价于
时,不等式①等价于 ,∴无解
,∴无解当
 时,不等式①等价于
时,不等式①等价于 ,即
,即 ,∴
,∴ ;
;综上函数
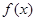 的定义域为
的定义域为 .
. (Ⅱ)∵函数
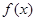 的定义域为
的定义域为 , ∴不等式
, ∴不等式 恒成立,
恒成立,∴只要
 即可,又
即可,又
(当且仅当
 时取等)
时取等)即
 ,∴
,∴ . ∴
. ∴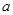 的取值范围是
的取值范围是 .
.点评:解决该试题的关键是利用绝对值的含义以及公式来分情况讨论求解得到,属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 轴相交。②奇函数的图像不一定过原点。③偶函数若在
轴相交。②奇函数的图像不一定过原点。③偶函数若在 上是减函数,则在
上是减函数,则在 上一定是增函数。④有且只有一个函数既是奇函数又是偶函数。其中正确结论的个数是( )
上一定是增函数。④有且只有一个函数既是奇函数又是偶函数。其中正确结论的个数是( )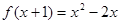 ,则
,则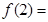 .
. 的定义域为
的定义域为 ,其中a、b为任
,其中a、b为任 时,研究
时,研究 其中k是正整数,对一切正整数k不等式
其中k是正整数,对一切正整数k不等式 都有解,求m的取值范围。
都有解,求m的取值范围。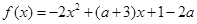 ,
,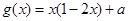 ,其中
,其中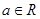 .
.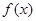 是偶函数,求函数
是偶函数,求函数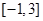 上的最小值;
上的最小值;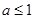 时,
时,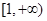 上为减函数;
上为减函数;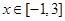 ,函数
,函数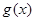 图象上方,求实数
图象上方,求实数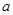 的取值范围.
的取值范围. 满足下述条件:对任意实数
满足下述条件:对任意实数 ,当
,当 时,总有
时,总有 ,则实数
,则实数 的取值范围是( )
的取值范围是( )



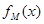 的定义域为R,且定义如下:
的定义域为R,且定义如下: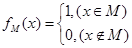 (其中M是实数集R的非空真子集),在实数集R上有两个非空真子集A、B满足
(其中M是实数集R的非空真子集),在实数集R上有两个非空真子集A、B满足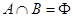 ,则函数
,则函数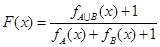 的值域为 ( )
的值域为 ( )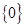
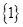
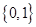
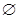
 是定义在实数集R上的不恒为零的偶函数,且对任意实数
是定义在实数集R上的不恒为零的偶函数,且对任意实数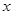 都有
都有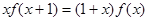 ,则
,则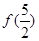 的值是( )
的值是( )



 由下表定义:
由下表定义:
 ,
, ,
, ,则
,则 .
.