题目内容
11．设偶函数f（x）在[0，+∞）上为增函数，则不等式f（x）＞f（2x十1）的解集为（ ）| A． | ∅ | B． | {x|x＜-1或x＞$\frac{1}{3}$} | C． | {x|x＞1或x＜$\frac{1}{3}$} | D． | {x|-1＜x＜-$\frac{1}{3}$} |
分析 利用偶函数的图象关于y轴对称，又且在[0，+∞）上为增函数，将不等式中的抽象法则f脱去，解不等式求出解集．
解答 解：∵f（x）是定义在R上的偶函数，
∴不等式f（x）＞f（2x十1）可化为不等式f（|x|）＞f（|2x十1|）
∵f（x）在[0，+∞）上为增函数
∴|x|＞|2x+1|
解得x＞$\frac{1}{3}$或x＜-1
故选：B．
点评 本题考查利用函数的对称性及函数的单调性脱抽象的法则，将抽象不等式转化为具体不等式解．
练习册系列答案
相关题目
2．一个公司的一款新产品有若干销售店，为了解该产品的广告投入费用与销售额间的关系，该公司抽取了其中的五个销售店作为样本，统计出它们的广告投入费用x与销售额y，如下表：
（1）求销售额y对广告费用x的线性回归方程$\widehaty=\widehatbx+\widehata$；
（2）设k=$\frac{销售额}{广告费}$，若k≥10，则称该店为“盈利店”，把上述样品中“盈利店”的频率视作一个店是“盈利店”的概率，现另外再调查3个销售店，记这三个店中“盈利店”的个数为X，求X的分布列和数学期望．
附：回归直线的斜率和截距的最小二乘法估计公式分别为：$\widehat{b}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}=\overline{y}-\widehat{b}\overline{x}$．
| x（万元） | 2 | 4 | 5 | 6 | 8 |
| y（万元） | 30 | 40 | 60 | 50 | 70 |
（2）设k=$\frac{销售额}{广告费}$，若k≥10，则称该店为“盈利店”，把上述样品中“盈利店”的频率视作一个店是“盈利店”的概率，现另外再调查3个销售店，记这三个店中“盈利店”的个数为X，求X的分布列和数学期望．
附：回归直线的斜率和截距的最小二乘法估计公式分别为：$\widehat{b}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}=\overline{y}-\widehat{b}\overline{x}$．
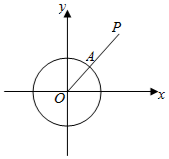在平面直角坐标系xOy中，对于⊙O：x2+y2=1来说，P是坐标系内任意一点，点P到⊙O的距离SP的定义如下：若P与O重合，SP=r；若P不与O重合，射线OP与⊙O的交点为A，SP=AP的长度（如图）．