题目内容
7．在平面直角坐标系xOy中，已知$x_1^2-ln{x_1}-{y_1}=0$，x2-y2-2=0，则${（{x_1}-{x_2}）^2}+{（{y_1}-{y_2}）^2}$的最小值为（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 化简已知条件，得到两个函数，利用函数的导数求出切线的斜率，利用平行线之间的距离求解即可．
解答 解：实数x1，y1，x2，y2满足$x_1^2-ln{x_1}-{y_1}=0$，x2-y2-2=0，
可得y1=x12-lnx1，并且x2-y2-2=0，
（x1-x2）2+（y1-y2）2的最小值转化为：
函数y=x2-lnx图象上的点与x-y-2=0图象上的点的距离的最小值的平方，
由y=x2-lnx可得y′=2x-$\frac{1}{x}$=$\frac{{2x}^{2}-1}{x}$，
与直线x-y-2=0平行的直线的斜率为1，
所以2x-$\frac{1}{x}$=1，解得x=1，
切点坐标（1，1），与x-y-2=0平行的直线为：y-1=x-1，即x-y=0，
而x-y=0和x-y-2=0的距离是$\sqrt{2}$，
（x1-x2）2+（y1-y2）2的最小值为：2．
故选：B．
点评 本题考查函数与方程的综合应用，函数的导数求解函数的最值，考查计算能力以及转化思想．
练习册系列答案
相关题目
如图，已知在△ABC中，AC的中点为E，AB的中点为F，延长BE至P，使BE=EP，延长CF至Q，使CF=FQ．试用向量方法证明P，A，Q三点共线．
15．执行如图的程序框图，输出S的值为（ ）
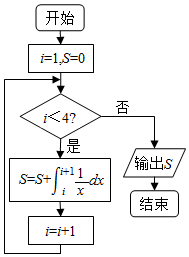
| A． | ln4 | B． | ln5 | C． | ln 5-ln4 | D． | ln 4-ln 3 |
2．函数f（x）=sin2x+2$\sqrt{3}$cos2x-$\sqrt{3}$，g（x）=mcos（2x-$\frac{π}{6}$）-2m+3（m＞0），若对任意x1∈[0，$\frac{π}{4}$]，存在x2∈[0，$\frac{π}{4}$]，使得g（x1）=f（x2）成立，则实数m的取值范围是（ ）
| A． | （1，$\frac{4}{3}$） | B． | （$\frac{2}{3}$，1] | C． | [$\frac{2}{3}$，1] | D． | [1，$\frac{4}{3}$] |
12．“a=0”是“函数f（x）=sinx-$\frac{1}{x}$+a为奇函数”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
19．已知${z_1}=2t+i，{z_2}=1-2i，若\frac{z_1}{z_2}$为实数，则实数t的值为（ ）
| A． | 1 | B． | -1 | C． | $\frac{1}{4}$ | D． | $-\frac{1}{4}$ |