题目内容
在数列{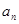 }中,
}中,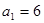 ,且
,且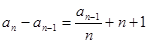
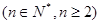 ,
,
(1)求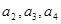 的值;
的值;
(2)猜测数列{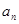 }的通项公式,并用数学归纳法证明。
}的通项公式,并用数学归纳法证明。
(1) (2)
(2)
解析试题分析:解:(1)
(2)猜测 。下用数学归纳法证明:
。下用数学归纳法证明:
①当 时,显然成立;
时,显然成立;
②假设当
 时成立,即有
时成立,即有 ,则当
,则当 时,由
时,由 得
得 ,
,
故
 ,故
,故 时等式成立;
时等式成立;
③由①②可知, 对一切
对一切 均成立。
均成立。
考点:数学归纳法
点评:本题用到的数学归纳法,在高中数学中常用来证明等式成立和数列通项公式成立。若要证明一个与自然数n有关的命题P(n),有如下步骤:
(1)证明当n取第一个值 时命题成立。
时命题成立。 对于一般数列取值为0或1,但也有特殊情况;
对于一般数列取值为0或1,但也有特殊情况;
(2)假设当n=k(k≥ ,k为自然数)时命题成立,证明当n=k+1时命题也成立。
,k为自然数)时命题成立,证明当n=k+1时命题也成立。
综合(1)(2),对一切自然数n(≥ ),命题P(n)都成立。
),命题P(n)都成立。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 和公比为
和公比为
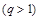 的等比数列
的等比数列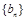 满足:
满足: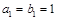 ,
,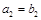 ,
, .
.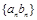 的前
的前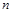 项和为
项和为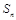 ,且对任意
,且对任意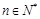 均有
均有 成立,试求实数
成立,试求实数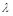 的取值范围.
的取值范围.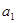 =2,点(
=2,点(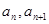 )在函数
)在函数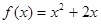 的图像上,其中
的图像上,其中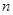 =
=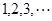 .
.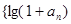 }是等比数列;
}是等比数列;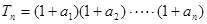 ,求
,求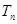 及数列{
及数列{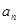 }的通项公式;
}的通项公式;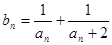 ,求数列{
,求数列{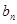 }的前n项和
}的前n项和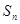 ,并证明
,并证明 .
.  ,规定
,规定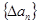 为数列
为数列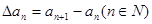 , 对自然数
, 对自然数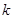 ,规定
,规定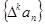 为
为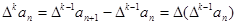 .
.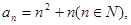 ,试判断
,试判断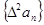 是否为等差或等比数列,为什么?
是否为等差或等比数列,为什么?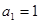 ,且满足
,且满足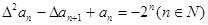 ,求数列
,求数列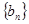 ,使得
,使得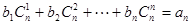 对一切自然
对一切自然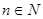 都成立?若存在,求数列
都成立?若存在,求数列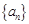 的各项都是正数,前
的各项都是正数,前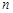 项和为
项和为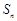 ,且对任意
,且对任意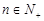 ,都有
,都有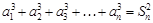 .
.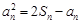 ; (2)求数列
; (2)求数列 为正常数,且
为正常数,且
 的通项公式;
的通项公式;
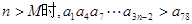 恒成立?若存在,求出相应的M的最小值;若不存在,请说明理由。
恒成立?若存在,求出相应的M的最小值;若不存在,请说明理由。 的前项和为
的前项和为 ,满足
,满足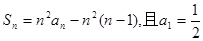 ,
,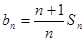 ,证明:
,证明: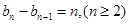 ;
;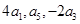 成等差数列.
成等差数列.