题目内容
已知等差数列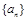 和公比为
和公比为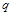
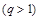 的等比数列
的等比数列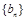 满足:
满足: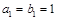 ,
,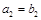 ,
, .
.
(Ⅰ)求数列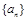 ,
,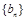 的通项公式;
的通项公式;
(Ⅱ)若数列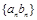 的前
的前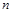 项和为
项和为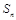 ,且对任意
,且对任意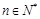 均有
均有 成立,试求实数
成立,试求实数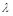 的取值范围.
的取值范围.
(Ⅰ)  ,
, ;(Ⅱ)
;(Ⅱ)  .
.
解析试题分析:(Ⅰ)设等差数列的公差为 ,根据题中条件,可以列出关于
,根据题中条件,可以列出关于 与
与 的方程组;(Ⅱ)典型的错位相减法求出
的方程组;(Ⅱ)典型的错位相减法求出 ,不等式变成
,不等式变成 ,然后利用右边数列的单调性即可.
,然后利用右边数列的单调性即可.
试题解析:(Ⅰ)设等差数列的公差为 ,根据题意,得
,根据题意,得 ,解得
,解得 (舍去),或
(舍去),或 ,
,
所以数列 ,
, 的通项公式分别为:
的通项公式分别为: ,
, . 5分
. 5分
(Ⅱ) ①
①
所以 ②
②
①-②,得 ,
,
∴ ; 9分
; 9分
所以 ,化简并整理,得
,化简并整理,得 . 10分
. 10分
令 ,则
,则 .
.
∵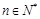 ,∴
,∴ ,∴对
,∴对 ,
, ,∴
,∴ ,故
,故 . 13分.
. 13分.
考点:等差数列与等比数列的概念与通项公式、数列求和、数列的单调性.

练习册系列答案
相关题目
 }满足
}满足 -
-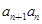 -2
-2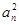 =0,n∈N﹡,且
=0,n∈N﹡,且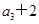 是a2,a4的等差中项.
是a2,a4的等差中项.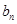 =
=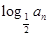 ,
,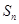 =b1+b2+…+
=b1+b2+…+ 同时满足:①不等式
同时满足:①不等式 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在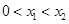 ,使得不等式
,使得不等式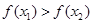 成立 设数列
成立 设数列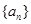 的前
的前 项和为
项和为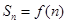
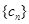 中,所有满足
中,所有满足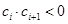 的正整数
的正整数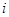 的个数称为这个数列
的个数称为这个数列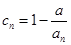 (
(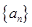 的前
的前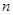 项和
项和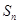 ,且
,且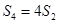 ,
,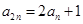 .
.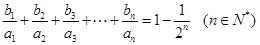 ,求数列
,求数列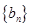 的前
的前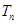 .
.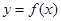 的图象经过坐标原点,其导函数为
的图象经过坐标原点,其导函数为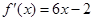 ,数列
,数列 的前
的前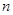 项和为
项和为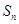 ,点
,点 均在函数
均在函数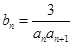 ,
, 是数列
是数列 的前n项和,求使得
的前n项和,求使得 对所有
对所有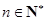 都成立的最小正整数
都成立的最小正整数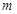 .
. 及其前
及其前 项和
项和 满足:
满足: (
( ,
,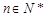 ).
). ,
, 是等差数列;(2)求
是等差数列;(2)求 及
及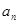 .
.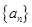 满足
满足 ,且
,且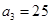 .
. 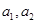
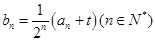 ,且{
,且{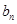 }为等差数列?若存在,求出t的值;若不存在,说明理由.
}为等差数列?若存在,求出t的值;若不存在,说明理由.  ,如果存在实常数
,如果存在实常数 使得
使得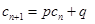 对于任意
对于任意 都成立,我们称数列
都成立,我们称数列 数列”.
数列”. ,
, ,
, 、
、 是否为“
是否为“ ,若不是,请说明理由;
,若不是,请说明理由; 也是“
也是“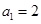 ,
,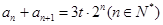 ,
, 为常数.求数列
为常数.求数列 项的和.
项的和.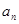 }中,
}中,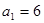 ,且
,且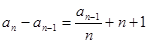
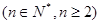 ,
,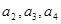 的值;
的值;