题目内容
已知数列 的前项和为
的前项和为 ,满足
,满足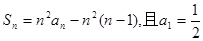 ,
,
(1)令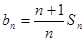 ,证明:
,证明: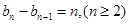 ;
;
(2)求数列 的通项公式。
的通项公式。
(1)利用已知的递推关系,将 表示即可得到。
表示即可得到。
(2)
解析试题分析:(1)根据题意,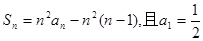 ,令
,令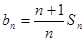 ,则可知
,则可知 ,故可知当
,故可知当 ,满足
,满足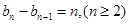 ;
;
(2)根据题意,由于数列 的前项和为
的前项和为 ,满足
,满足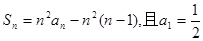 ,那么可知
,那么可知 =
= 
考点:数列的通项公式的求解
点评:主要是考查了数列的前n项和与其通项公式的关系的运用,属于基础题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
已知数列 的前项和为
的前项和为 ,满足
,满足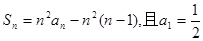 ,
,
(1)令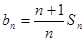 ,证明:
,证明: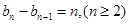 ;
;
(2)求数列 的通项公式。
的通项公式。
(1)利用已知的递推关系,将 表示即可得到。
表示即可得到。
(2)
解析试题分析:(1)根据题意,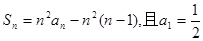 ,令
,令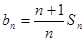 ,则可知
,则可知 ,故可知当
,故可知当 ,满足
,满足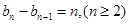 ;
;
(2)根据题意,由于数列 的前项和为
的前项和为 ,满足
,满足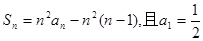 ,那么可知
,那么可知 =
= 
考点:数列的通项公式的求解
点评:主要是考查了数列的前n项和与其通项公式的关系的运用,属于基础题。

 名校课堂系列答案
名校课堂系列答案