题目内容
（本小题共14分）
已知椭圆
的焦点是
,
,点
在椭圆上且满足
.
（Ⅰ）求椭圆的标准方程；
（Ⅱ）设直线
与椭圆的交点为
，
.
(i)求使
的面积为
的点的个数；
(ii)设
为椭圆上任一点，
为坐标原点，
，求
的值.
（本题满分14分）
解：（Ⅰ）∵
>
∴点
满足的曲线
的方程为椭圆
∵
∴
∴椭圆的标准方程为
. …………………4分
（Ⅱ）(i) ∵ 直线
与椭圆的交点为
，
∴
,
若
∴
∵原点
到直线的距离是
∴在直线的右侧有两个符合条件的点
设直线
与椭圆相切，则
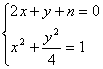有且只有一个交点
∴
有且只有一个解
由
解得
（设负）
此时，
与
间距离为
∴在直线的左侧不存在符合条件的点
∴符合条件的点有2个. …………………10分
(ii)设
，则
满足方程：
∵
∴
即：
，从而有
∴
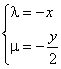
. …………………14分
练习册系列答案
名校名卷单元同步训练测试题系列答案
相关题目
的前n项和为
，点
在直线
是等差数列；
满足
，求数列
，求证：
的底面是正方形，
，点E在棱PB上。
； 
且E为PB的中点时，求AE与平面PDB所成的角的大小。
的离心率为
，右准线方程为
的方程；
是圆
上动点
处的切线，
，证明
的大小为定值.
底面ABCD，PD=DC，点E是PC的中点，作EF
的棱长为
，
是
与
的交点，
为
的中点．
∥平面
；
平面
；
的体积．