题目内容
0＜α＜π，sinα+cosα=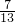
，则1-
=
- A.
- B.
- C.
- D.
D
分析：方程sinα+cosα=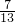两边平方，求出sinαcosα，转化为cosa-sina，利用正切和正弦、余弦的关系化简1-，整体代入求解即可．
解答：2sinacosa=（sina+cosa）2-1=-
（cosa-sina）2=1-2sinacosa=
0＜a＜π，cosa＜sina
∴cosa-sina=-
1-=
=
=
故选D．
点评：本题考查同角三角函数间的基本关系，弦切互化，考查计算能力，逻辑推理能力，是基础题．
分析：方程sinα+cosα=
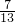两边平方，求出sinαcosα，转化为cosa-sina，利用正切和正弦、余弦的关系化简1-，整体代入求解即可．解答：2sinacosa=（sina+cosa）2-1=-
（cosa-sina）2=1-2sinacosa=
0＜a＜π，cosa＜sina
∴cosa-sina=-
1-
===故选D．
点评：本题考查同角三角函数间的基本关系，弦切互化，考查计算能力，逻辑推理能力，是基础题．
练习册系列答案
相关题目
设直线ax+by+c=0的倾斜角为α，且sinα+cosα=0，则a，b满足（ ）
| A、a+b=1 | B、a-b=1 | C、a+b=0 | D、a-b=0 |