题目内容
已知函数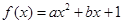 在
在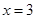 处的切线方程为
处的切线方程为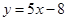 .
.
(1)求函数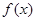 的解析式;
的解析式;
(2)若关于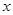 的方程
的方程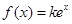 恰有两个不同的实根,求实数
恰有两个不同的实根,求实数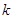 的值;
的值;
(3)数列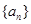 满足
满足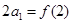 ,
,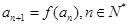 ,求
,求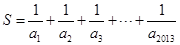 的整数部分.
的整数部分.
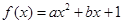 在
在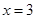 处的切线方程为
处的切线方程为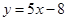 .
.(1)求函数
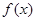 的解析式;
的解析式;(2)若关于
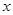 的方程
的方程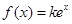 恰有两个不同的实根,求实数
恰有两个不同的实根,求实数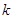 的值;
的值;(3)数列
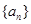 满足
满足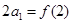 ,
,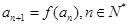 ,求
,求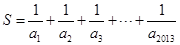 的整数部分.
的整数部分.(1) ;(2)
;(2)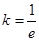 或
或 ;(3)
;(3) .
.
 ;(2)
;(2)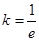 或
或 ;(3)
;(3) .
.试题分析:(1)由题意可得
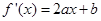 ,又根据
,又根据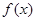 在
在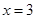 处的切线方程为
处的切线方程为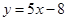 ,故可从切线斜率
,故可从切线斜率 与切点
与切点 建立关于
建立关于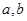 的方程组
的方程组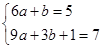 ,可解得
,可解得 ,从而
,从而 ;(2)由(1)及方程
;(2)由(1)及方程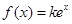 ,参变分离后可得:
,参变分离后可得: ,因此问题就等价于求使恰有两个不同的
,因此问题就等价于求使恰有两个不同的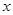 ,满足
,满足 的
的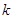 的值,令
的值,令 ,
,可得
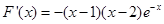 ,从而当
,从而当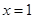 时,
时,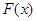 取极小值
取极小值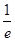 ,当
,当 时,
时,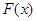 取极大值
取极大值 ,因此可以大致画出
,因此可以大致画出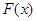 的示意图,而问题则进一步等价于直线
的示意图,而问题则进一步等价于直线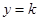 与
与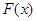 的图像恰有两个交点,通过示意图易得当
的图像恰有两个交点,通过示意图易得当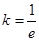 或
或 时满足题意;(3)通过题意可知,需求得
时满足题意;(3)通过题意可知,需求得 的值夹在哪两个整数之间,由(1)
的值夹在哪两个整数之间,由(1) ,可得
,可得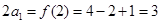 ,因此
,因此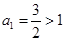 ,而
,而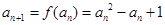 ,
,∴
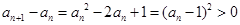 ,∴
,∴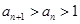 ,而将递推公式
,而将递推公式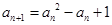 可进一步变形为
可进一步变形为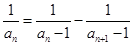 ,从而
,从而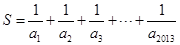
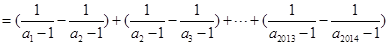
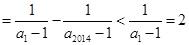 ,
,又有
 ,从而
,从而 的整数部分为
的整数部分为 .
.试题解析:(1)∵
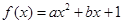 ,∴
,∴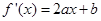 , 由题意
, 由题意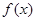 在
在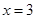 处的切线方程为
处的切线方程为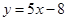 ,则
,则 ,∴
,∴ ;
;(2)由(1)
 ,∴
,∴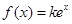 即
即 ,∴
,∴ ,因此问题即等价于存恰有两个不同的
,因此问题即等价于存恰有两个不同的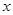 ,使,令
,使,令
 ,则
,则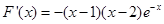 ,∴
,∴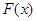 在
在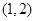 上单调递增,在
上单调递增,在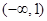 ,
, 上单调递减,∴当
上单调递减,∴当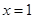 时,
时,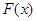 取极小值
取极小值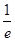 ,当
,当 时,
时,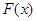 取极大值
取极大值 ,又当
,又当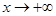 时,
时,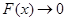 ,当
,当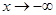 时,
时,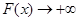 ,因此可画出函数
,因此可画出函数 的大致示意图如下,而问题就等价于直线
的大致示意图如下,而问题就等价于直线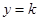 与
与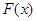 的图像恰有两个交点,
的图像恰有两个交点,
故要存在两个不同的
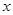 满足
满足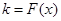 ,则需
,则需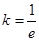 或
或 .
.(3)由(1)
 ,∴
,∴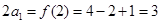 ,∴
,∴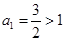
又∵
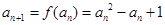 ,∴
,∴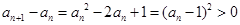 ,
,∴
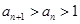
由
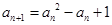 ,得
,得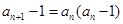 ,∴
,∴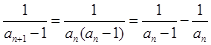 ,
,即
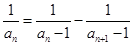 ,
,∴
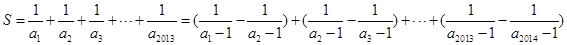
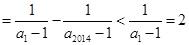 ,又∵
,又∵ ,
, 综上,
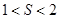 ,∴
,∴ 的整数部分为
的整数部分为 .
.
练习册系列答案
相关题目
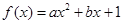 (
(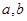 为实数,
为实数,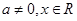 ),
),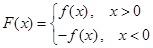 ,⑴若
,⑴若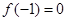 ,且函数
,且函数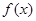 的值域为
的值域为 ,求
,求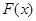 的表达式;
的表达式;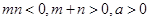 ,且函数
,且函数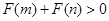 是否大0?
是否大0?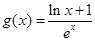 ,当
,当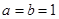 时,证明:对任意实数
时,证明:对任意实数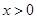 ,
,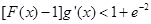 (其中
(其中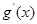 是
是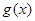 的导函数) .
的导函数) .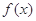 定义在
定义在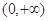 上的非负可导函数,且满足
上的非负可导函数,且满足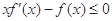 ,对任意正数
,对任意正数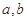 , 若
, 若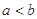 ,则必有( ).
,则必有( ).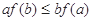



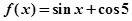 ,则该函数在点
,则该函数在点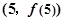 处切线的斜率等于( )
处切线的斜率等于( )



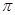 为圆周率,
为圆周率,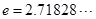 为自然对数的底数.
为自然对数的底数.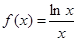 的单调区间;
的单调区间;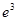 ,
,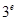 ,
,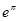 ,
,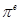 ,
,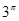 ,
,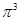 这6个数中的最大数与最小数;
这6个数中的最大数与最小数;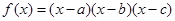 ,(
,(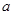 、
、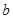 、
、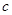 是两两不等的常数),则
是两两不等的常数),则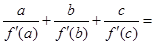 .
. ;③(ex)′=ex;④(
;③(ex)′=ex;④( )′=x;⑤(x·ex)′=ex+1.
)′=x;⑤(x·ex)′=ex+1.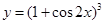 的导数。
的导数。